Você trabalha no departamento de segurança do site de um banco. Para acessar suas contas, os clientes devem criar uma senha de 8 dígitos, como mostra a Figura 3.22. Sua função é determinar os requisitos de senha para as contas. Os procedimentos de segurança determinam que, para que o site seja seguro, a probabilidade de uma senha de 8 dígitos ser adivinhada em uma tentativa deve ser menor que , assumindo que todas as senhas são igualmente prováveis. Seu trabalho consiste em usar as técnicas de probabilidade que você aprendeu neste capítulo para decidir quais requisitos um cliente deve atender ao escolher sua senha, incluindo que conjunto de caracteres são permitidos, de modo que o site seja seguro de acordo com os procedimentos de segurança.

Segurança adicional

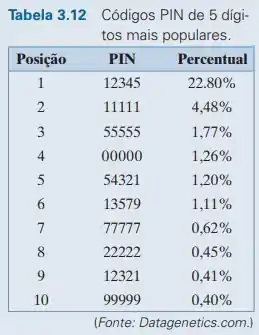
Para segurança adicional, cada cliente cria um código PIN (número de identificação pessoal) de 5 dígitos. A Tabela 3.12 mostra os 10 códigos PIN de 5 dígitos mais comumente escolhidos. Da tabela pode ser verificado que mais de um terço de todos os códigos de 5 dígitos poderiam ser adivinhados tentando esses 10 números. Para desencorajar os clientes de utilizar códigos previsíveis, você considera proibir códigos PIN que usam o mesmo dígito mais de uma vez.

(a) Como essa exigência afetaria o número de códigos PIN possíveis?

(b) Você decidiria proibir PINs que usam o mesmo dígito mais de uma vez? Explique.

Passo 1

Passo 2

Resposta