Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 30
ABCD é um paralelogramo e é uma das suas diagonais. Os pontos X e Y são tais que . Demonstre que XDYB é um paralelogramo.
Passo 1
Fala, galera! Essa questão é um pouquinho complicada de entender no início, mas nada que um desenho não ajude a melhorar. Pode ser que não tenham interseção entre si, como na figura abaixo.
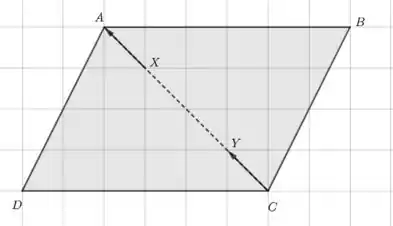
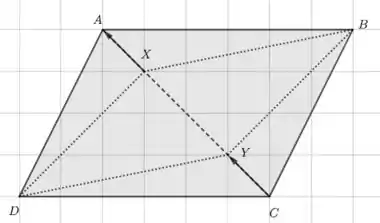
Também pode acontecer algo do tipo:
O importante é que tenham mesmo módulo, direção e sentido para que seja válido. Podemos ver claramente através das duas figuras que XDYB é um paralelogramo, mas como provar isso? Fica ligado no próximo passo.
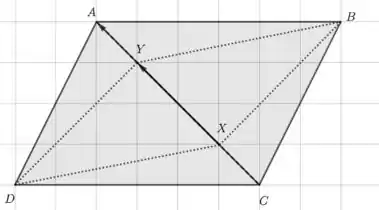
Passo 2
Para demonstrar que XDYB é paralelogramo, temos que provar que que lados opostos são paralelos e de mesmo tamanho, ou seja, e . Vamos levar em consideração a terceira figura do Passo 1, mas o raciocínio para a quarta figura seria o mesmo. Então vamos lá, escrevendo todos os vetores em termos de e , obtemos:
onde usamos o fato de que , que já foi dado no enunciado e porque ABCD é um paralelogramo. Continuando:
onde, novamente, usamos o fato de que . Com isso, conseguimos demonstrar que XDYB é paralelogramo.
Resposta
Ver a resolução acima.