Equações Básicas na Forma Integral para um Volume de Controle

CARAMBA!!! Equações Básicas na Forma Integral para um Volume de Controle?

Assunto com o nome grande, não é? Assusta?

Mas calma, o nome é grande, porém o assunto não é tão complicado assim quanto parece.

Aqui nós estamos na matéria Mecânica dos Fluidos, então vamos abordar esse assunto no contexto de escoamento de fluidos, beleza?

Primeiramente, é importante a gente entender o que seria o chamado Volume de Controle. O volume de controle, também chamado carinhosamente de VC, é a região do espaço, escolhida por nós, que engloba o escoamento do fluido que iremos analisar.

Para você entender melhor, dá uma olhada aqui nessa imagem, na qual o fluido escorre da região A para a região B:

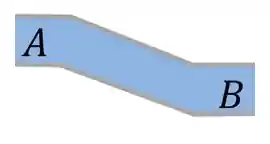
Qual região do espaço escolheríamos para ser nosso VC? A que está em laranja? em roxo? ou em vermelho?

É importante a gente escolher uma região que a gente consiga analisar o escoamento como um todo, ou seja, consiga analisar propriedades no início e no final do escoamento.

Isso ocorre se escolhermos a região em vermelho, pois ela pega a região A, na qual o fluido começa escoando, e pega também a região B, para a qual o fluido escoa, e assim conseguimos ver o escoamento como um todo, sacou?

Beleza, mas para que temos que escolher um volume de controle?

Que bom que você está se questionando isso. Escolhemos o volume de controle porque é essa região que vamos analisar e aplicar as equações básicas para conseguirmos informações sobre o escoamento.

Existem diversas coisas que queremos saber sobre o escoamento como: velocidade, vazão mássica, vazão volumétrica, pressão, etc.

E é aí que entram as equações básicas na forma integral para um volume de controle. Como o próprio nome já diz são equações na forma integral que serão aplicadas no volume de controle para descobrirmos uma propriedade.

A vazão volumétrica, por exemplo, ela é representada por e calculada através da seguinte equação:

Onde:

• é a área da superfície transversal ao escoamento;
• é a velocidade de escomento do fluido sobre a superfície de área e;
• a vazão volumétrica, expressa em unidade de volume por tempo.

Similarmente, podemos encontrar a vazão mássica, :

Onde:

• é a área da superfície transversal ao escoamento;
• é a velocidade de escomento do fluido sobre a superfície de área e;
• é a densidade do fluido que está escoando, e;
• a vazão mássica, expressa em unidade de massa por tempo.

Deu pra começar a entender o assunto não é mesmo?

Essa é uma parte bem inicial e mais tranquila, mas não precisa de desesperar porque temos aqui todo o conteúdo que precisa. Vai aprender sobre a equação de Bernoulli, Princípio da Continuidade e muitas outras coisas.

Confere o nosso Raio-X aqui em seguida. Você vai ver todo o nosso conteúdo organizado e separado para você estudar tudo de maneira rápida e descontraída e arrasar na prova. 👇🏽