Calcule a área do paralelogramo definido pelos vetores .
Passo 1
Vamos começar relembrando o que significa dizer “módulo do vetor ”:
O módulo do vetor é dado por
E o produto vetorial de dois vetores, você se lembra?
O produto vetorial de é dado por :
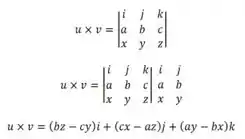
Mas, qual a razão de lembrar tudo isso? Simplesmente para podermos entender melhor a fórmula da área de um paralelogramo definido por dois vetores:
Passo 2
Agora vamos calcular o produto vetorial para :
Substituindo , temos:
Passo 3
Então, temos que a área do paralelogramo será:
Só falta calcularmos o módulo desse vetor!