Um cisalhamento na direção y é a transformação matricial f:R2 → R2 definida por f(v) = Av, e
e k é um escalar. Seja R o retângulo definido no Exercício 2 e seja f o cisalhamento na direção y com k = -2. Encontre e esboce a imagem de R.
Passo 1
E aí pessoal, belezinha. Vamos agora trabalhar em algumas questões de computação gráfica, envolvendo transformações lineares.
A partir do enunciado, sabemos que um cisalhamento, sendo , na direção y, é uma transformação linear dada por:
Passo 2
Para realizarmos o cisalhamento dos pontos dados, com k = -2, teremos que:
E calculamos as imagens f(v1), f(v2), f(v3) e f(v4):
Passo 3
Os vértices do retângulo, cisalhado na direção do eixo y, são (1, -1), (1, 2), (3, -5) e (3, -2).
O retângulo antes do cisalhamento:
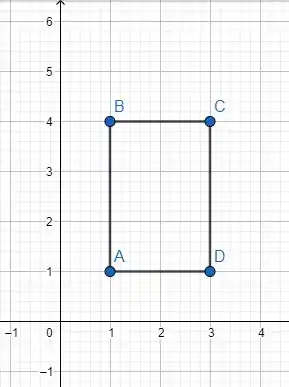
Após o cisalhamento:
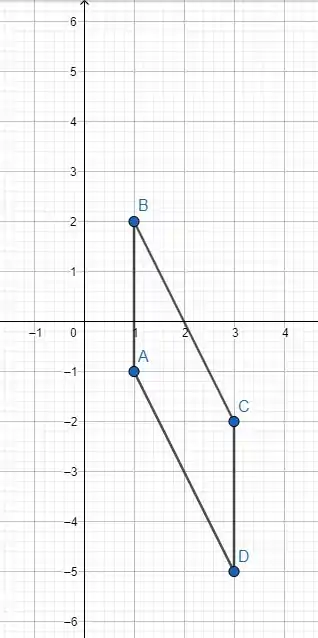
Resposta
Ver passo a passo.