Considere a matriz
(a) Desenhe um grafo que tenha A como matriz de adjacência. Não se esqueça de marcar os vértices no gráfico.
(b) Analisando o grafo, determine o número de caminhos de comprimento 2 de , a e de , a .
(c) Calcule a segunda linha de A³ e use-a para determinar o número de caminhos de comprimento 3 de , a e de , a .
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
a)
Lembre-se que a (i,j) entrada da matriz A representa uma linha beterraba entre os pontos e . O gráfico deve ser assim:
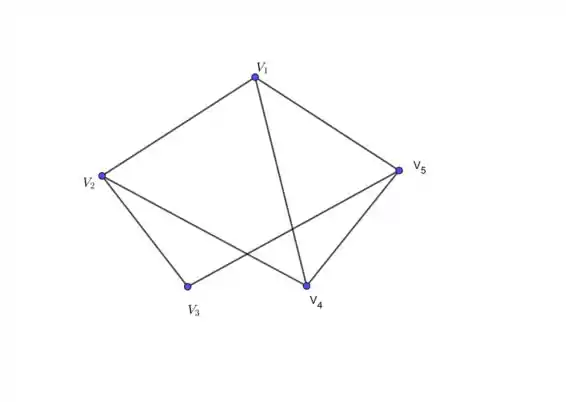
Passo 2
b) A partir do vértice , há seguintes passeios de comprimento 1:
No entanto, não há caminhadas de comprimento de 1 de , ou para . Assim, não há caminhadas de comprimento de 2 de para .
No entanto, não há caminhadas de comprimento de 1 de , ou para . Assim, não há caminhadas de comprimento de 2 de para
Passo 3
c) Desde , a fim de calcular a segunda linha da matriz , só precisamos calcular a segunda linha de e multiplicá-lo com A. A fim de calcular a segunda linha de precisamos multiplicar a segunda linha da matriz A consigo mesma. Vamos denotar a segunda linha da matriz com e a segunda linha da matriz A com . Nós temos o seguinte
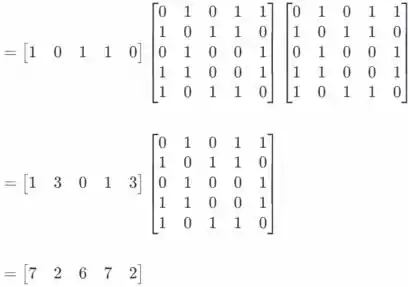
Há 2 caminhadas de comprimento 3 de para
.
Resposta
Resposta nos passos.