Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo Exercícios Adicionais.3 - Ex. 86

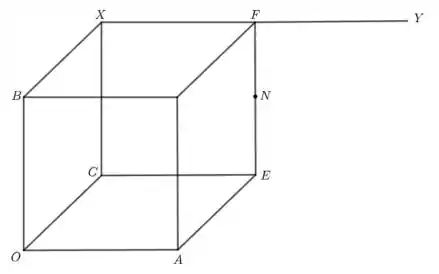
O cubo, ao lado, tem aresta de comprimento 1 (um). N é o ponto médio de E F → .

  1. Determine as coordenadas de O N → na base ( O A → , O B → , O C → ) .
  2. Qual é a norma de O N → ?
  3. Sendo X F → = F Y → , quais são as coordenadas e a norma de A Y → ?

Passo 1

  1. Fala, galera! Nós podemos escrever o vetor O N → como soma dos vetores

    2. O N → =   O A → +   A E → +   E N →

    Como os lados paralelos de um cubo são iguais, então A E → = O C → e E F → = O B → . Além disso, N é o ponto médio de E F → , ou seja,   E N → = 1 2   E F → = 1 2 O B → . Assim, ficamos com

    O N → =   O A → +   A E → +   E N → =   O A → + O C →   + 1 2 O B → = ( 1 , 1 2 , 1 )

    Passo 2

  2. Para calcular a norma de O N → vamos usar O N → =   ( 1 , 1 2 , 1 ) . Assim,

    3. | O N → | = 1 + 1 4 + 1   = 9 4 = 3 2

    Até que não foi muito difícil, não é mesmo?

    Passo 3

  3. Para obter A Y → , precisamos somar alguns vetores

A Y → = A E → + E F → + F Y →

Do item a), já sabemos que A E → = O C → e E F → = O B → . Além disso, o enunciado nos deu X F → = F Y → , mas X F → = O A → . Então F Y → = O A → . Assim, vamos escrever A Y → na base ( O A → , O B → , O C → ) :

A Y → = O C → + O B → + O A → = ( 1,1 , 1 )

Agora podemos calcular a norma de A Y → :

| A Y → | = 1 + 1 + 1 = 3

Resposta

  1. O N → = ( 1 , 1 2 , 1 )
  2. | O N → | = 3 2
  3. A Y → = ( 1,1 , 1 ) , | A Y → | = 3