Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo Exercícios Adicionais.3 - Ex. 79

Demonstre: Se a → e b → são vetores quaisquer, então:

  1. a → ⋅ b → = 1 4 ( | a → + b → | 2 - | a → - b → | 2 ) ;
  2. | a → + b → | 2 + | a → - b → | 2 = 2 ( | a → | 2 + | b → | 2 ) . Interprete geometricamente.

Passo 1

  1. Galerinha, nessa questão é mais fácil a gente calcular | a → + b → | 2 e | a → - b → | 2 , subtrair uma da outra, dividir por quatro e mostrar que é igual a a → ⋅ b → . Temos

    2. | a → + b → | 2 = ( a → + b → ) ⋅ ( a → + b → ) = | a → | 2 + 2 a → ⋅ b → + | b → | 2

    | a → - b → | 2 = ( a → - b → ) ⋅ ( a → - b → ) = | a → | 2 - 2 a → ⋅ b → + | b → | 2

    Vamos subtrair a segunda equação da primeira

    | a → + b → | 2 - | a → - b → | 2 = | a → | 2 + 2 a → ⋅ b → + | b → | 2 - ( | a → | 2 - 2 a → ⋅ b → + | b → | 2 ) = 4 a → ⋅ b →

    Agora, só precisamos dividir por quatro e a identidade fica mostrada:

    1 4 ( | a → + b → | 2 - | a → - b → | 2 ) = a → ⋅ b →

    Passo 2

  2. Para esse item, vamos somar | a → + b → | 2 e | a → - b → | 2 ao invés de subtrair. A parte boa é que já calculamos esses termos no passo anterior, então só precisamos somar:

| a → + b → | 2 + | a → - b → | 2 = | a → | 2 + 2 a → ⋅ b → + | b → | 2 + | a → | 2 - 2 a → ⋅ b → + | b → | 2 = 2 ( | a → | 2 + | b → | 2 )

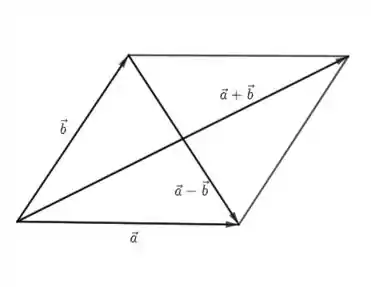
Prontinho! A parte algébrica até que não foi complicada, mas agora temos que interpretar geometricamente. Basicamente, a → + b → é o vetor soma de a → e b → e a → - b → é o vetor diferença. Podemos ver que a → + b → e a → - b → são as diagonais de um paralelogramo formado por a → e b → . Isso quer dizer que a soma dos quadrados das diagonais de um paralelogramo é igual a duas vezes a soma dos quadrados dos lados.

Resposta

Veja a resolução acima.