Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 6.3 - Ex. 8
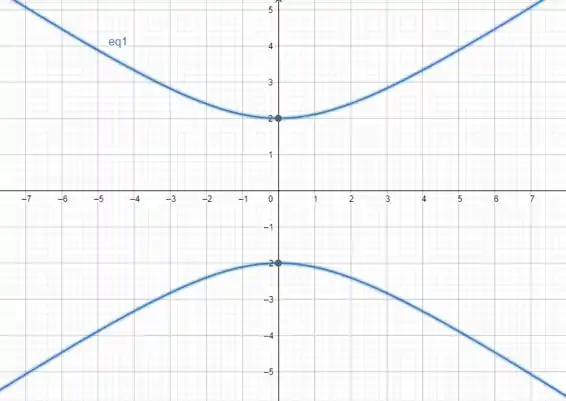
Identificar a cônica, achar a equação no último sistema de coordenadas utilizado e fazer um esboço do gráfico.
Passo 1
E aí, aluno?! Vamos para mais uma questão!
Podemos reescrever a equação como
Tal que
Passo 2
Calculando o polinômio característico da matriz A:
p(λ) =
Igualando a zero e resolvendo:
Esses são os nossos autovalores, determinando os autovetores, que podem ser ortonormalizados:
E para o segundo autovalor:
Dessa forma, podemos dizer que temos:
e
Tal que .
Passo 3
Realizando uma mudança de variável de X = PX’, em que
Podemos reescrever
Como
Dessa forma:
Realizando as devidas manipulações algébricas e voltando as variáveis para x e y, obtemos, então:
Que podemos reescrever como:
Dividindo por 36:
Que pode ser escrito como:
Assim, temos a fórmula de uma hiperbole.
Resposta
Hiperbole
