Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear e Aplicações (Reginaldo J. Santos)- Ed: 1º - Capítulo 4.3 - Ex. 10
Identificar a cônica, achar a equação no último sistema de coordenadas utilizando e fazer um esboço do gráfico.
Passo 1
E aí galerinhaaa, blz?
Esse exercício tem por objetivo desenvolver nossas habilidades em encontrar as equações da cônicas...
Veja que a equação pode ser escrita como tal que e .
Agora, borá lá calcular o polinômio característico da matriz .
Sabemos que
Passo 2
Agora, vamos determinar os autovalores e seus autovetores associados.
Perceba que os autovalores são e . Já os autovetores associados ao autovalor são as soluções não nulas do sistema , ou ainda. , cuja solução é . Já a base ortonormal em relação a é dada por , isto é, . E os autovetores associados ao autovalor são as soluções não nulas do sistema , ou ainda. , cuja solução é . Temos que é a base ortonormal de , ou seja, .
Sabemos que , onde e .
Passo 3
Fazendo uma mudança de variável , onde na equação .
Assim, .
Isto é, .
Obtemos, , ou ainda,
Realizando novamente uma mudança de variável, onde e , teremos que a equação da cônica é dada por , ou ainda na forma padrão temos, .Perceba que a cônica é uma hipérbole.
Já o gráfico da quádrica é dado por:
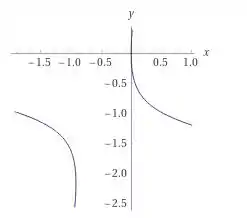
Resposta
Cônica: hipérbole;equação:.