São dados , Escreva em função de e
Passo 1
Fala ae, galera! Blz? 😊
Vamos analisar a imagem abaixo para entender bem o problema.
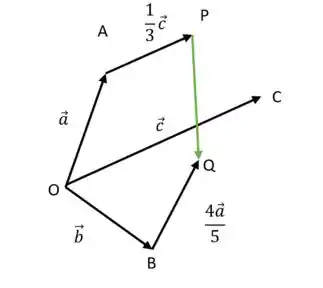
Passo 2
Para acharmos o vetor , teremos que realizar a adição de vetores. Portanto:
São dados , Escreva em função de e
Fala ae, galera! Blz? 😊
Vamos analisar a imagem abaixo para entender bem o problema.

Para acharmos o vetor , teremos que realizar a adição de vetores. Portanto: