Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo Exercícios Adicionais.3 - Ex. 69
São dados: , e .
- Que tipo de quadrilátero é determinado pelos pontos e ? (paralelogramo? losango? retângulo? trapézio?). Faça um desenho.
- Determine o coseno do menor ângulo formado pelas diagonais. (Sugestão: determine todos os seis vetores da figura. )
Passo 1
- Fala, pessoal! Vamos começar calculando cada um dos vetores que representam as arestas desse quadrilátero. Depois, vamos calcular os módulos desses vetores (ou seja, o tamanho das arestas) e o ângulo entre dois deles, caso seja necessário. Já temos e , então só faltam
- Para descobrir qual o menor ângulo formado pelas diagonais precisamos calcular os vetores das diagonais. Já temos , então só falta
Os módulos dos vetores são:
Como todas as arestas têm lados diferentes, podemos descartar as seguintes possibilidades: paralelogramo, losango e retângulo. Além disso, , ou seja, esses lados são paralelos. Assim, temos um trapézio, cujas base tem tamanho e . O desenho fica mais ou menos assim
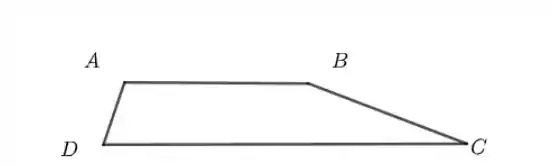
Passo 2
Além disso,
As duas diagonais formam dois ângulos diferentes. Para encontrá-los, só precisamos mudar o sentido do vetor de alguma das diagonais:
Quando o ângulo está entre , o cosseno do ângulo vai de a e quando o ângulo está entre o seu cosseno vai de a . Então, o menor ângulo será o que tem sinal positivo, ou seja, .
Resposta
- Trapézio