Seja C o conjunto dos números complexos e sejam x = a + bi e y = c + di dois elementos de C. Considere a relação R sobre C definida por:
- Mostre que R é uma relação de ordem parcial sobre C.
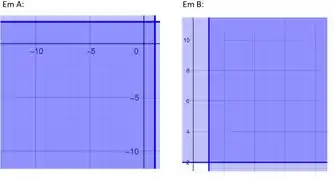
- Assinale no plano Argand-Gauss o conjunto A dos complexos z tais que zR(1 + 2i) e o conjunto B dos complexos z tais que (1 + 2i)Rz.
- Decida: C é totalmente ordenado por R?
Passo 1
Fala minha galera, bora fazer mais um exercício maravilhoso da matemática discreta!
- Dessa vez precisamos saber se ela é reflexiva, antissimétrica e transitiva para que a relação seja de ordem parcial, então bora lá!
- Vamos nessa fazer uma figura utilizando o Geogebra! Como temos pela definição dada no problema, tendo tal que , então e para o primeiro caso e para o segundo caso e . Agora vamos plotar as figuras sendo o conjunto dos vetores com origem e (0,0), e o conjunto .
- Para que seja totalmente ordenado por R, ou , visto isso temos duas hipóteses:
Já podemos concluir de cara que a relação é reflexiva pois dado com x e y tal como descrito no enunciado, então:
Supondo agora que então , temos que as seguintes relações são válidas:
Mas isso só pode existir se a = c e b = d, logo ela é antissimétrica, pois x = y somente em um caso.
E a transitividade é atestada com o um tal que , assim:
Dessa forma, e, analogamente, , implicando que . Dessa forma concluímos que a relação é de ordem parcial.
Passo 2
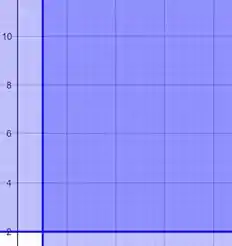 Em A:Em B:
Em A:Em B:
Passo 3
E é muito simples contrariar, basta que existam x e y tal que
Particularmente, podemos pensar em , ou seja, existem dois números tal que a relação não exista. Portanto R não pode ser totalmente ordenado.
Resposta
- Demonstração
- Não é totalmente ordenado.