Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Geometria Analítica - Reis e Silva- Ed: 2º - Capítulo 4.Exercícios - Ex. 30

Sejam u   e   v vetores unitários e perpendiculares entre si. Demonstre que | | u   × v | |   =   1 .

Passo 1

Sejam os vetores u = ( a , b , c )   e   v = ( x , y , z ) , temos que o produto vetorial u × v será:

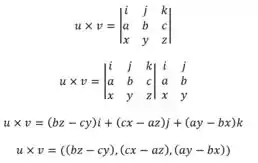
Assim, u × v = ( b z - c y ) 2 + ( c x - a z ) 2 + ( a y - b x ) 2

E, u × v 2 = ( b z - c y ) 2 + ( c x - a z ) 2 + ( a y - b x ) 2 =

= b 2 z 2 - 2 b c z y + c 2 y 2 + c 2 x 2 - 2 c a z x + a 2 z 2 + a 2 y 2 - 2 b a y x + b 2 x 2 ( 1 )

Passo 2

Além disso, temos que :

| | u | | 2 = ( a 2 + b 2 + c 2 ) 2 = a 2 + b 2 + c 2 e | | v | | 2 = ( x 2 + y 2 + z 2 ) 2 = x 2 + y 2 + z 2 e ( u . v ) 2 = ( a x + b y + c z ) 2 = a 2 x 2 + b 2 y 2 + c 2 z 2 + 2 a b x y + 2 a c x z + 2 b c y z

Então, | | u | | 2 | | v | | 2 - ( u . v ) 2 = a 2 + b 2 + c 2 x 2 + y 2 + z 2 - a 2 x 2 - b 2 y 2 - c 2 z 2 - 2 a b x y - 2 a c x z - 2 b c y z

| | u | | 2 | | v | | 2 - ( u . v ) 2 = b 2 z 2 - 2 b c z y + c 2 y 2 + c 2 x 2 - 2 c a z x + a 2 z 2 + a 2 y 2 - 2 b a y x + b 2 x 2

| | u | | 2 | | v | | 2 - ( u . v ) 2 = b 2 z 2 - 2 b c z y + c 2 y 2 + c 2 x 2 - 2 c a z x + a 2 z 2 + a 2 y 2 - 2 b a y x + b 2 x 2   ( 2 )

Passo 3

E, comparando as equações ( 1 )   e   ( 2 ) , temos:

u × v 2 = | | u | | 2 | | v | | 2 - ( u . v ) 2  

Como os vetores u   e   v   são unitários, | | u | | = 1   e   | | v | | = 1   . E,   u   e   v são perpendiculares se, e somente se, u   .   v   =   0 .

Então, u × v 2 = 1 2 . 1 2 - ( 0 ) 2 = 1 - 0 = 1  

| | u × v | | = 1 = 1 como queríamos provar.

Resposta

Ei, a resposta está no passo a passo :)