Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 3

Sendo a → = O A → e b → = O B → dois vetores não paralelos, escreva v → = O P → como combinação linear de a → e b → , sabendo que A P → = 2 3 A B →

Passo 1

Fala ae, galera! Blz? 😊

Vamos analisar a imagem abaixo para entender bem o problema

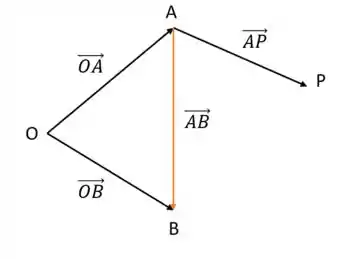
Passo 2

Precisamos definir quem é o vetor A B → .

Pela subtração de vetores, temos que:

A B → = - O A → + O B →

Agora, precisamos definir o vetor O P → .

Pela soma de vetores, temos que:

O P → = O A → + A P →

Passo 3

Como A P → = 2 3 A B → , substituindo:

O P → = O A → + 2 3 A B →

Agora, substituindo A B → = - O A → + O B → :

O P → = O A → + 2 3 - O A → + O B →

Assim:

O P → = 1 3 O A → + 2 3 O B →

Como O P → = v → ,   O A → = a → e O B → = b → , temos:

v → = 1 3 a → + 2 3 b →

Resposta

v → = 1 3 a → + 2 3 b →