Use o gráfico para estimar o máximo absoluto, o mínimo absoluto e os extremos locais.
Passo 1
FALAAAA, ESTUDANTE!
Eu sei, é normal se confundir em exercícios conceituais, e isso costuma piorar um pouco quando temos gráficos para analisar. Mas confia na gente e não se preocupa, vai dar certo!
Primeiro, o que são os máximos e mínimos de uma função?
Um ponto de uma função é chamado de máximo se for maior que os pontos próximos dele, e é chamado de mínimo se for menor que esses pontos.Ou seja, podemos ter vários máximos e mínimos na mesma função, beleza?
E o que é máximo absoluto? Também chamado de máximo global, como você pode ter visto na nossa seção de Cálculo I, é quando o ponto é maior que TODOS os outros na função.
Já o mínimo absoluto (ou mínimo global) é quando o ponto é menor que todos os outros na função.
Mas como assim, o ponto ser maior ou menor?!

Imagina que eu tenho uma função f(x).Vou selecionar dois pontos aleatórios de abscissa c e d. Se f(c) > f(d), então o ponto de abscissa c é maior que o ponto de abscissa d, beleza? De modo semelhante, se f(c)
Outra coisa que ele pede são os extremos locais. O que é isso? São os máximos e mínimos locais, ou seja, os outros máximos e mínimos que não os globais.
Ufa! Agora que temos todos esses conceitos, bora pra questão!
Passo 2
Antes de tudo, vamos procurar o máximo absoluto no gráfico.
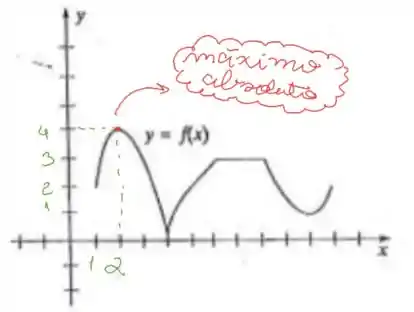
Se você traçar uma reta horizontal a partir do ponto vermelho, vai ver que não vai capturar mais nenhum ponto do gráfico. Portanto, temos o máximo absoluto, que é o maior ponto do gráfico. Considerando cada tracinho como 1 unidade, esse ponto tem coordenadas x = 2 e y = 4, ou seja, (2, 4).
Passo 3
Já o mínimo absoluto:
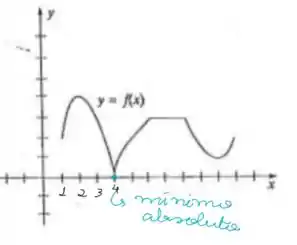
Em azul, temos o mínimo absoluto, que toca o eixo x (só disso já sabemos que y = 0) e está em x = 4. Portanto, é o ponto (4, 0)
Passo 4
Agora, os extremos locais:
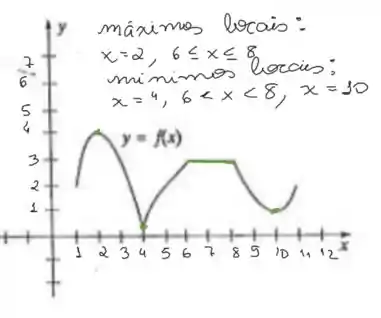
Note que os máximos e mínimos globais não deixam de ser, também, locais. Isso porque são maiores/menores que os pontos próximos, ou seja, entram na definição, por isso, x = 2 e x = 4 entram :)
Em casos de trecho constante, ele será tanto máximo quanto mínimo local.
E aí? Viu que não era nenhum bicho de 7 cabeças? Pratique e arrase, pequeno(a) gafanhoto! :)
Resposta
Máximo absoluto: (2, 4);
Mínimo absoluto: (4, 0);
Extremos locais: máximos (x = 2, 6 x 8) e mínimos (x = 4, 6