Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 5

A B C D é um trapézio, A B → = a → ,   D C → = 2 a → e D A → = b → . O ponto E é tal que B E → = 1 3 B C → . Escreva A C → e D E → em função de a → e b → .

Passo 1

Fala ae, galera! Blz? 😊

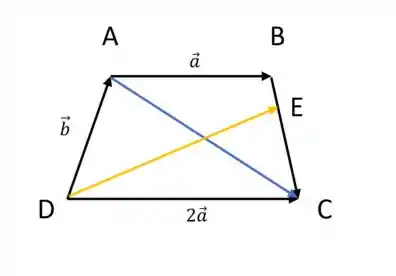
Vamos analisar a imagem abaixo para entender bem o problema.

Passo 2

Precisamos definir quem é o vetor B C → .

Pela adição de vetores, temos que:

B C → = - a → - b → + 2 a → = a → - b →

Passo 3

Agora, conseguimos dizer quem é A C → .

Diagonal A C → :

A C → = - b → + 2 a →

Como B E → = 1 3 B C → , D E → será:

D E → = 2 a → - 2 3 B C →

D E → = 4 a → + 2 b → 3

Resposta

A C → = - b → + 2 a →

D E → = 4 a → + 2 b → 3

Exercícios de Livros Relacionados

Verifique se é verdadeira ou falsa cada afirmação e justifique sua resposta ( A , B ) ∈ A B → A , B~C , D ↔ A B → = C D → A B // C D→ A B→ // C D → A B → = C D →→ A = CeB = D .
Prove que u → = 0 → ↔u → = 0
Prove que A , B ~ P , QeC , D ~ P , Q → A , B ~ ( C , D ) .
Prove que -u → =u →
Mostre que, se A≠ B , então A , B e B , A são de mesmo comprimento, mesma direção e sentido contrário.