1.Determine o domínio da função dada por
Esboce os gráficos de e .
b)
Passo 1
O domínio de é o conjunto de todos os para os quais a sequência converge. Sendo assim temos que proceder da seguinte forma:
Como temos uma indeterminação do tipo infinito sobre infinito, podemos aplicar L’H.
Logo,
Passo 2
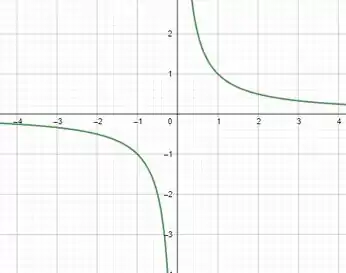
O esboço do gráfico de para um dos valores de x é dado por:
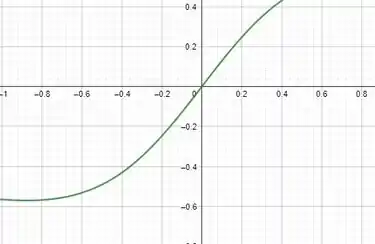
Passo 3
O esboço do gráfico de é dado por: