Calcule e interprete geometricamente o resultado obtido
Letra e)
Onde é o circulo
Onde
Passo 1
O circulo que representa a superfície é
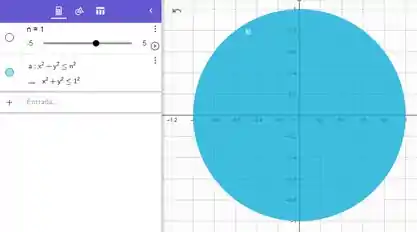
Passo 2
Vamos resolver este limite composto por uma integral dupla na forma polar onde, o ângulo varia de a .
O raio obedece a restrição
Logo
E os diferenciais serão substituídos por
Passo 3
Desta forma a integral pode ser reescrita como
Ou ainda
Passo 4
Aplicando ao limite
A primeira parcela é igual a zero, dessa forma