Considere a competição entre o peixe azulado e o vermelhão mencionada no Problema Suponha que de modo que, como mostrado no texto, existe um ponto de equilíbrio estavel no qual ambas as espécies podem coexistir. E conveniente reescrever as equações do Problema em termos das capacidades de saturação do lago para o peixe azulado na ausência de vermelhão e para o vermelhão () na ausência do peixe azulado.
a) Mostre que as equações do Problema tomam a forma:
,
Onde e . Determine o ponto de equilíbrio de coexistência ( X,Y) em função de B,R, e .
b) Suponha, agora, que um pescador só pesca o peixe azulado, o que reduz B. Qual o efeito disso nas populações de equilíbrio? É possível, pescando, reduzir a população do peixe azulado a um tal nível que ele será extinto?
Passo 1
Saudações galerinha! Tudo bem?
Vamos juntos resolver mais um exercício?
Bora lá começar então!
Primeiramente vamos organizar e reescrever nossas variáveis x:
Primeiramente vamos organizar e reescrever nossas variáveis y:
Até aí tranquilo?

O ponto de equilíbrio de coexistência é dado por:
e
Essas equações podem ser resolvidas aplicando o determinante, utilizada no problema anterior. Beleza!
Suas soluções serão:
Passo 2
Se B for reduzido, fica claro pela resposta do item (a) que é reduzido e é aumentado. Para determinar se o peixe azul vai morrer. Vamos fazer a seguinte analise.
Inicialmente devemos observar que e
Para analisar melhor o comportamento dessas espécie vamos traçar as curvas de modelam seu comportamento.
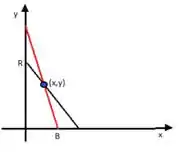
De acordo como indicado na figura, onde estão os pontos críticos indicado por pontos pesados. À medida que diminui, diminui, aumenta (como indicado acima) e o ponto de interseção aproxima-se de . Se coexistência não é possível e o único os pontos críticos são Pode-se mostrar que são instáveis e é assintoticamente estável. Daí concluímos, quando coexistência não é mais possível, que e e assim a população de do peixe azul morrerá.
Te vejo na próxima questão!