Determinar o campo de existência das funções:
Passo 1
Para determinar o campo de existência das funções, vamos analisar quais valores pode assumir, para que assuma valores reais.
Sabemos que a condição de existência de um logaritmo, é, para
a base deve ser um número positivo e diferente de 1, e o logaritmando deve ser um número positivo maior que zero. Logo:
Vamos encontrar as raízes do numerador:
Podemos começar testando se a divisão do termo independente pelo termo que acompanha o terceiro grau é raíz da equação:
Sabemos que é uma raíz da equação. Vamos aplicar agora Briot Ruffini.
Vamos lembrar como fazemos Briot Ruffini.
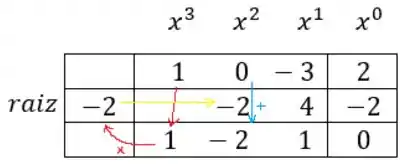
Montamos o quadro, com os coeficientes dos termos da equação em cima , e a primeira raiz que acabamos de testar a esquerda .Descemos com o primeiro coeficiente , e multiplicamos pela raiz , preenchendo com o resultado na linha do meio, abaixo do segundo coeficiente .
Fazemos a soma vertical e colocamos o resultado na linha de baixo , esse mesmo resultado multiplicaremos pela raiz novamente, e preenchemos na linha do meio .
Novamente fazemos a soma vertical e preenchemos o resultado embaixo , esse mesmo resultado que multiplicamos pela raiz novamente.
O produto dessa multiplicação , colocamos abaixo do último coeficiente , e assim fazemos a última soma vertical.
Encontrando zero, temos os coeficientes da equação de segundo grau que precisaremos encontrar a raiz:
Fazendo bháskara:
Logo, as duas raízes encontradas também serão raiz da nossa equação de terceiro grau.
Lembrando da nossa equação:
Sendo então e as raízes que zeram a equação. Vamos testar valores maiores e menores, para saber sobre o sinal do termo.
Para :
Para :
Para :
Para o termo do denominador, sabemos que não pode ser igual a , pois zera o termo. Então para o termo será negativo, e para o termo será positivo.

Logo, para que o logaritmando seja positivo, deve estar no intervalo e .
Resposta
Então, o campo de existência da função é:
Compreendeu toda a analisa dos sinais da função?
Montar a tabela ajuda muito nisso.