Determine um numero positivo sigma para o épsilon dado tal que |f(x)-L|> e sempre que 0
5 f(x) = 25x2-1 / 5x-1, a=-1/5, L=-2, e=0,01
Passo 1
Opa galeeeeera! Hoje vamos ver mais um pouco sobre a definição precisa de limites.
O enunciado nos pede para achar um valor positivo de , para o limite de com tendendo a .
Vamos começar desenhando o gráfico da função para termos uma intuição melhor.
E também vamos marcar o ponto , e tracejar até a reta da função e achar os valores de , ) e marcar o ponto , assim como representado a baixo.
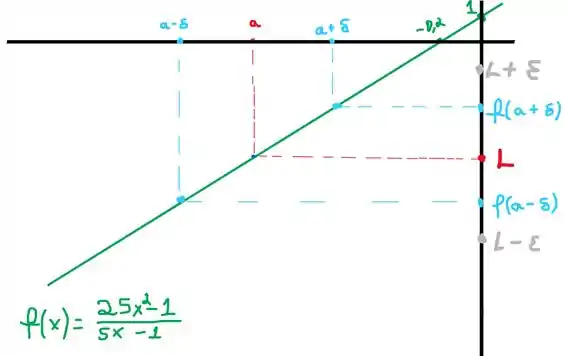
Passo 2
Vamos calcular o valor de cada um destes:
O enunciado diz que , e que Então:
Agora precisamos encontrar algum valor de de forma que quando pegarmos e esses dois valores estejam dentro do intervalo encontrado .
Para isso poderemos utilizar claramente um (relativamente menor do que o , e vamos testar se os valores de pegarmos e estão no intervalo pedido.
Passo 3
Assim:
Substituindo os valores:
E o valor superior:
Como ambos os valores encontrados estão muito distantes do intervalo pedido , não há tal para este intervalo... O valor de L está errado na verdade esse limite daria 0.
Resposta
Ei, a resposta está no passo a passo :)