Passo 1
Fala, galeeera!
Vamos esboçar o gráfico dessa curva para . Essa parte é fácil, né?
Vou montar uma tabelinha para ajudar a gente:
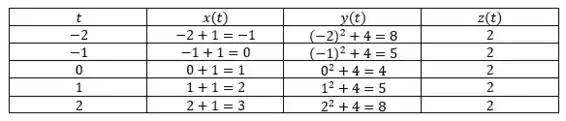
Lembrando que limitamos um valor arbitrário para fazer a tabela, porém .
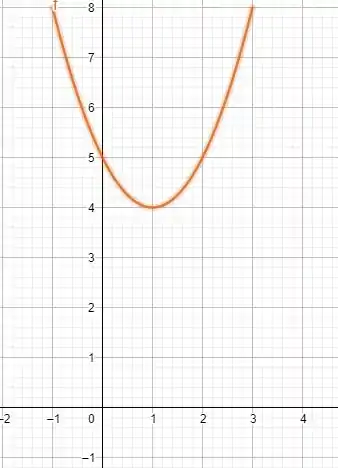
Agora é só traçar os pontos e esboçar nosso gráfico, mas pra ficar mais fácil de visualizar, vamos plotar em , pois em a figura está contida no plano .
Só para vocês terem uma ideia de como fica no espaço:
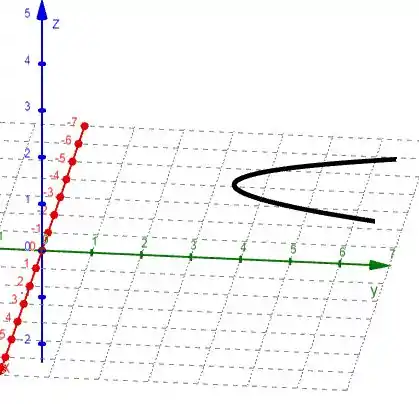
Passo 2
Nessa parte ele tá pedindo pra gente determinar a equação CARTESIANA da curva.
Bem, já nos foi dada a equação paramétrica da nossa curva.
E como fazemos para encontrar as equações cartesianas? Bem, basta eliminar o das nossas equações. Para isso iremos isolar em uma delas e substituir na outra, beleza?!
Substituindo em , temos;
Logo,
Essa é a nossa equação cartesiana.
Resposta
Esboço do gráfico descrito nos passos acima.
A equação cartesiana é: