Nos Exercícios 15-28, resolva as inequações e faça um esboço do gráfico da solução na reta real.
Passo 1
Primeiramente, devemos notar que a inequação acima é uma inequação de 2º grau. Ela pode ser reescrita como
onde somamos e em ambos os lados da inequação. Agora precisamos obter a solução de para fatorar o lado esquerdo da inequação. Pela fórmula de Bhaskara, temos
Deste modo, vemos que podemos reescrever . Ou seja,
Passo 2
Agora, precisamos analisar o sinal de para saber se a condição será satisfeita. Para tanto, vamos ver o sinal de e nos intervalos
, , .
Se o resultado da multiplicação for maior ou igual a num determinado intervalo, então a inequação não é válida nesse intervalo.
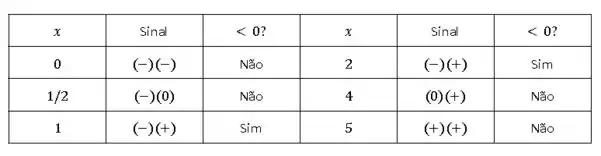
Ou seja, o único intervalo no qual a inequação é válida é . O mesmo resultado pode ser observado no gráfico da inequação, que é dado abaixo:
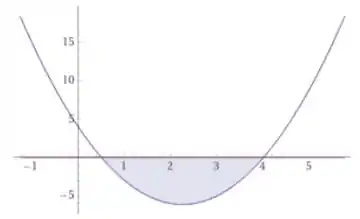
O intervalo na reta real no qual a inequação é válida é dado abaixo:

onde a bola vazia representa o intervalo aberto e temos que e .
Resposta
e o conjunto solução é o intervalo