Nos Exercícios 9-32, determine os números críticos e os intervalos abertos nos quais a função é crescente ou decrescente. Então, use uma ferramenta gráfica para traçar o gráfico da função.
Passo 1
Vamos começar calculando a derivada da função para depois calcular os pontos em que ela se anula, ou seja, os números críticos:
Então, é o único número crítico dessa função.
Passo 2
Como é número crítico, então temos dois intervalos de teste: e . Nesses intervalos, a função se comporta se seguinte forma:
Nesse intervalo, temos , ou seja,
,
onde invertemos a inequação no último passo porque multiplicamos por um número negativo. Assim, vemos que , isto é, a função é crescente nesse intervalo.
Nesse caso, temos . Seguindo de maneira similar ao caso anterior
,
encontramos que , o que indica que a função é decrescente nesse intervalo.
Passo 3
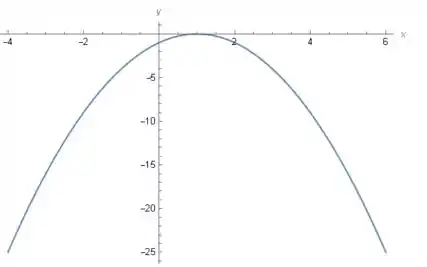
O gráfico da função está dado abaixo e condiz com o que obtivemos:
Resposta
é crescente em e decrescente em , com número crítico .