Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 12.Exercícios práticos - Ex. 70

Identifique e esboce as superfícies nos Exercícios 65-76.

70. y = - ( x 2 + z 2 )

Passo 1

E aí, pessoal! Bora lá para mais uma questão?

Na questão anterior, a gente tinha uma equação muito parecida com essa e mostramos que a superfície era um parabolóide elíptico. Calma, já já vamos relembrar o que é isso. Nessa questão, nós temos x e z elevados ao quadrado, e y não. Então, temos mais ou menos a equação:

x 2 a 2 + z 2 b 2 = y c

Tranquilo até agora? Acompanha aí o raciocínio no próximo passo.

Passo 2

Fazendo a = b = 1 e c = - 1 , a gente fica com

x 2 1 + z 2 1 = - y ⇒   y = - ( x 2 + z 2 )

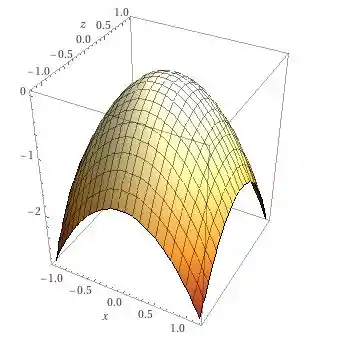
Ou seja, a superfície é um parabolóide elíptico, só que as parábolas tem a abertura na direção y . Também dá pra ver isso pela figura abaixo:

E aí, gostou dessa questão? Responde Aí!

Resposta

Parabolóide elíptico.