O lado de um quadrado mede L. Determinar o quadrado de área máxima que pode ser circunscrito no quadrado dado.
Passo 1
Primeiramente, desenharemos a situação apresentada e determinaremos os vínculos matemáticos encontradas através da geometria do problema, assim:
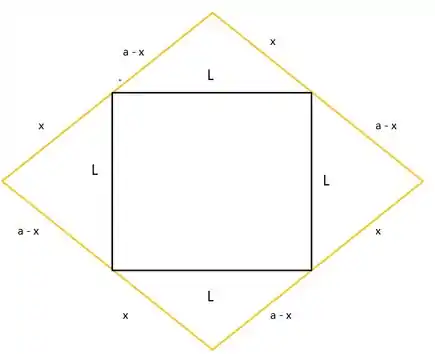
A área do quadrado circunscrito (amarelo), será:
Sendo ‘‘a’’ a aresta do quadrado.
Passo 2
Como esse quadrado está circunscrito em um quadrado menor de lado L, podemos obter uma relação entre a sua aresta e o lado do quadrado interior. Como os ângulos internos em um quadrado são iguais a 90°, nós temos 4 triângulos retângulos de lados ‘‘x’’, ‘‘a - x’’ e ‘‘L’’, assim, por Pitágoras:
Assim, obtemos uma relação entre o lado do quadrado interior (L) e as medidas do quadrado exterior (a e x).
Passo 3
Feito isso, como queremos maximizar a área do quadrado circunscrito, basta derivarmos a área do quadrado externo em função de a e igualar isso a zero. Assim encontraremos os pontos críticos da função. Logo:
Derivando,
Jogando isso na relação obtida pelo Pitágoras, temos:
Como L e x são positivos,
Passo 4
Substituindo x na aresta na relação encontrada pelo teorema de Pitágoras, temos:
Como ‘‘a’’ é positivo e diferente de zero,