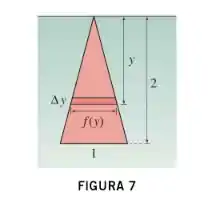
Uma placa em forma de triângulo isósceles com 1 pé de base e 2 pés de altura está submersa verticalmente num tanque d’água de modo que seu vértice toca a superfície d’água (Figura 7)
a) Mostre que a largura do triângulo à profundidade é .
b) Considere uma faixa estreita de altura à profundidade . Explique por que a força de fluido nessa faixa estreita é aproximadamente igual a , onde
c) Escreve uma aproximação para a força de fluido total num lado da caixa como uma soma de Riemann e indique a integral para a qual ela converge.
d) Calcule .
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A – Usando similaridade de triângulos, nós temos que
B – A pressão na altura está
e a área da faixa é aproximadamente
portanto, a força do fluido em um lado desta tira é aproximadamente dada por
Passo 2
C – Nesse caso, nós temos o seguinte somatório
O que dá aproximadamente
Quando , a soma de Riemann converge para
Passo 3
D- Nós temos que a força é igual a
Com isso, nós temos que
Logo,