Um recipiente tem forma de cone circular reto. A altura é 10 pés e o raio da base 4 pés. Lança-se água no recipiente na razão de 5 pés cúbicos por minuto. Com que velocidade se eleva o nível da água quando a profundidade da água é de 5 pés se:
a.O vértice do cone está para cima?
b.O vértice do cone está para baixo?
Passo 1
Bom, para começar essa questão vamos fazer um desenho para ajudar na resolução.
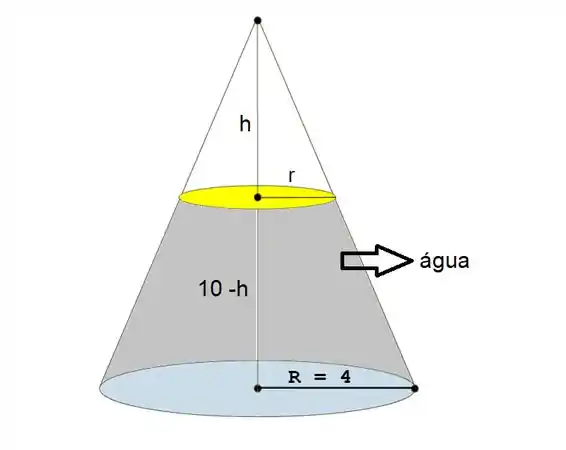
Por semelhança (olhando o triangulo com altura h e base r e o triangulo com altura 10 base 4) temos:
Passo 2
Agora usaremos a fórmula do volume de cone circular reto para calcular o volume de água:
Pela fórmula do volume
Como nós temos que o volume aumenta de 5 pés cúbicos por minuto, sabemos a taxa de variação do mesmo, ou seja, a derivada.
Agora basta derivar a equação:
Veja que é pedido , além disso
Substituindo tudo:
Passo 3
Para o caso do vértice para baixo é bem similar, porém o que antes não tinha água, agora terá e o que tinha, não terá mais.
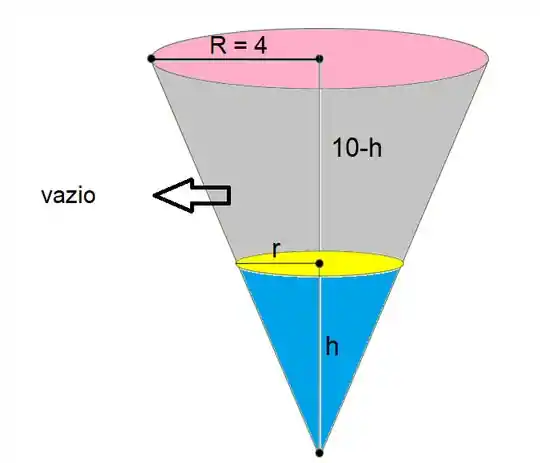
Veja agora que não precisamos nos preocupar em relacionar o volume do cone pequeno com o cone maior, pois já temos uma fórmula para o volume de água (é um cone de altura h e raio r).
Ainda vale a mesma relação de:
Vamos calcular o volume desse cone, sabendo que
Derivando:
Como queremos no momento em que h = 5, vamos substituir:
Resposta
Ambos itens tem mesma resposta: