O sistema mola-massa do Problema , suponha que a força exercida pela mola não e dada pela lei de Hooke, mas, em vez disso, satisfaz a relação:
Onde e é pequeno em módulo, mas pode ter qualquer sinal. A mola é considerada "dura" se e "mole" se . Por que esses termos são apropriados?
a) Mostre que o deslocamento da massa a partir de sua posicao de equilíbrio satisfaz a equação diferencial
Suponha as condições iniciais
No restante deste problema suponha
b) Encontre quando e determine, também a amplitude e o período do movimento.
c) Seja Faça o gráfico de uma aproximação numérica da solução. Esse movimento parece ser periódico? Se for, estime a amplitude e o período.
d) Repita o item (c) para e
e) Coloque em um gráfico os valores estimados da amplitude A e do período T em função de . Descreva a maneira segundo a qual A e T, respectivamente, dependem de .
f) Repita os itens (c), (d) e (e) para valores negativos de
Passo 1
Saudações galerinha! Tudo bem?
Vamos juntos resolver mais um exercício!
Bora lá começar então!
A força restauradora exercida pela mola é:
Em oposição a essa força restauradora em um força viscosa dada por:
Agora com base na segunda lei de Newton, com o sentido positivo para a direita temos:
Unido as equações:
Que simplificando temos a equação e aplicando as condições iniciais:
Tranquilo?
Vamos continuar então!
Passo 2
Com os valores de parâmetro especificados, a equação do movimento:
Possui solução geral:
Aplicando as condições iniciais
Logo a amplitude para a função seno é e o período do movimento é
Passo 3
Dado a equação do movimento é:
A solução desta EDO é dada de forma numérica. Através dela podemos estimar que:

Esboçando o gráfico teremos:
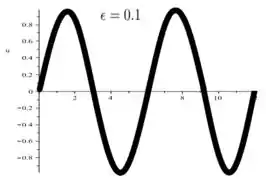
Passo 4
Dado a equação do movimento é:
A solução desta EDO é dada de forma numérica. Através dela podemos estimar que:
Dado a equação do movimento é:
A solução desta EDO é dada de forma numérica. Através dela podemos estimar que:
Esboçando o gráfico teremos:
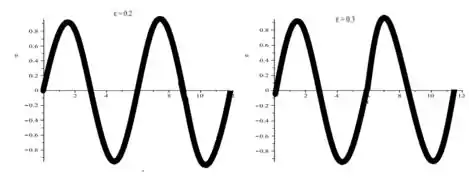
Até aí tranquilo?
Quase acabando continua por aqui, beleza!
Como o período T depende de .
A amplitude e o período parecem diminuir.
Firmeza, tudo bem?

Beleza, vamos continuar então!
Passo 5
Dado a equação do movimento é:
A solução desta EDO é dada de forma numérica. Através dela podemos estimar que:
Dado a equação do movimento é:
A solução desta EDO é dada de forma numérica. Através dela podemos estimar que:
Dado a equação do movimento é:
A solução desta EDO é dada de forma numérica. Através dela podemos estimar que:
Esboçando o gráfico teremos:
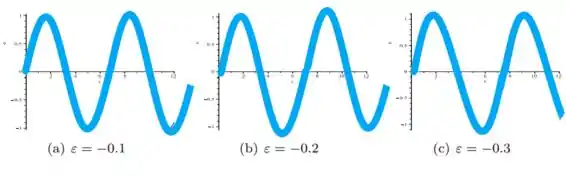
Ufa essa foi longa!
Te vejo na próxima questão!
Resposta
b) Amplitude para a função seno é e o período do movimento é