Suponha contínua, descrescente e positiva. Inspirado no método de Fermat (veja Exercício 22 da Seção 2.1) suponho , mostre que

Vamos antes de mais nada, abrir nossa somatória para podermos analisar melhor.

Então tome que

Supondo descrever nossa função como

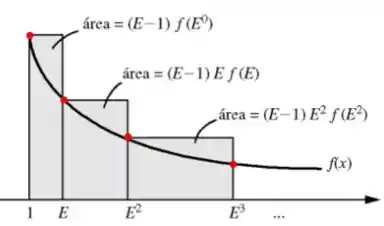
Onde os pontos vermelhos, são referentes aos nossos termos da somatória. Podemos escrever uma nova somatória dada por

Então temos que, se nossa somatatória for convergente, então pelo teste da comparação, temos que nossa função também será convergente.