Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.1 - Ex. 23

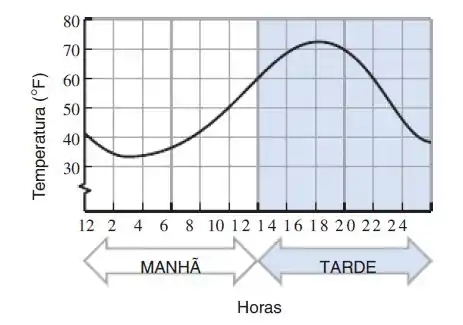
Suponha que na figura a seguir esteja a curva de temperatura externa em °F versus tempo relativa a um período de 24 horas.

  1. Estime a temperatura máxima e o instante no qual ela ocorre.
  2. O aumento da temperatura entre 8 h e 14 h é razoavelmente linear. Estime a taxa segundo a qual a temperatura está aumentando durante esse período.
  3. Estime o tempo no qual a temperatura decresce mais rapidamente. Estime a taxa de variação instantânea da temperatura em relação ao tempo naquele instante.

Passo 1

  1. Para estimar a temperatura máxima e o instante no qual ela ocorre basta olhar no gráfico onde há o maior pico, vemos que ocorre em T = 72 ° F , e ocorre as 4 horas da tarde.

    2. Passo 2

  2. Aqui a estimativa da taxa segundo a qual a temperatura está aumentando durante esse período vamos achar da seguinte forma:

    3. m = f x 1 - f x 2 x 1 - x 2

    Vamos então pegar os pontos em 8 e 14 horas:

    8,42 e 14,68

    Substituindo:

    m = f x 1 - f x 2 x 1 - x 2 = 42 - 68 8 - 14 = - 26 - 6 = 4,333 ° F / h

    Passo 3

  3. Olhando o gráfico vemos que o tempo no qual a temperatura decresce mais rapidamente é por volta de 9 horas da noite.

Para achar a taxa de variação instantânea da temperatura em relação ao tempo nesse instante, t = 9 , vamos achar a inclinação da reta tangente:

m = f x 1 - f x 2 x 1 - x 2

Vamos então pegar os pontos em 9 e 8 horas da noite:

9,53 e 8,60

Agora é só substituir:

m = f x 1 - f x 2 x 1 - x 2 = 53 - 60 9 - 8 = - 7 1 = - 7 F / h

Resposta

  1. T = 72 ° F e 4 horas da tarde
  2. 4,333 ° F / h
  3. 9 horas da noite e - 7 F / h
Ver Outros Exercícios desse livro