No triângulo de base e altura está inscrito um retângulo. Exprimir a área deste retângulo como função da sua base .
Construir o gráfico desta função e achar seu valor máximo.
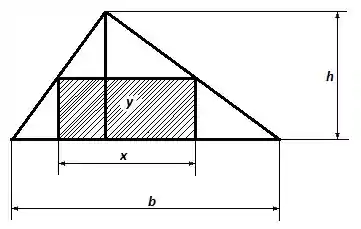
Passo 1
Primeiro, devemos enxergar que a base do retângulo é também a base do triângulo menor formado sobre ele:
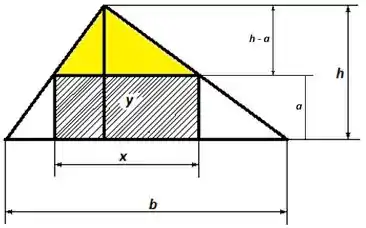
Adotamos como altura do retângulo inscrito, logo, a altura do triângulo menor será .
A relação das bases dos triângulos tem a mesma proporção que as alturas dos mesmos.
Assim:
Manipulando, podemos encontrar a altura , do retângulo:
Assim, temos a área:
Passo 2
O gráfico da função que expressa a área do retângulo é:
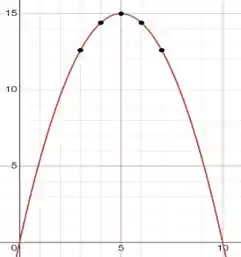
A partir da curva, temos o ponto máximo , sendo o valor de o valor da base onde o retângulo inscrito tem sua área máxima possível.
Resposta
Com , o valor máximo de área possível do retângulo é .