Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton, Bivens, Davis - Cálculo Vol 2- Ed: 10º - Capítulo 14.3 - Ex. 10

Use uma integral dupla em coordenadas polares para calcular a área da região descrita: a região no interior do círculo x 2 + y 2 = 4 e a direita da reta x = 1 .

Passo 1

Olá galera! Lembrem-se que os problemas deste tipo se resolvem aplicando a seguinte fórmula

á r e a   d e   R = ∬ R 1   d A = ∬ R d A

onde R é a área duma região do plano xy.

Passo 2

Sendo assim, só nos resta esboçar a região R com a finalidade de conhecer os intervalos onde r e θ varia. Boraaa encontrar esses intervalos!

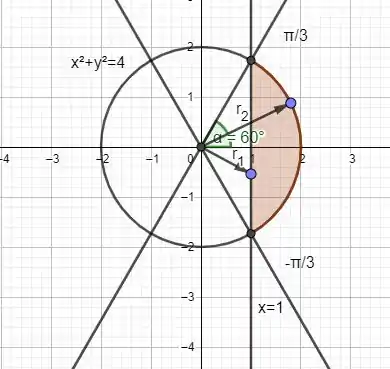
Primeiro precisamos encontrar os pontos de interseção da circunferência x 2 + y 2 = 4 com a reta x = 1 . Para tal precisamos de substituir x = 1 na equação de circunferência. Assim, teremos

1 + y 2 = 4

y 2 = 3

y = ± 3

Como tg ⁡ α = y x = ± 3 1 ⟺ θ = ± π 3 .

Olhando o esboço da região R podemos notar que r 1 ≤ r ≤ r 2 e - π 3 ≤ θ ≤ π 3 . Sendo assim, devemos conhecer os raios r 1 e r 2 para podermos calcular esta área. Como o raio r 2 é o raio do círculo, então r 2 = 2 . Para calcular o r 1 devemos usar a seguinte fórmula r 2 = x 2 + y ² , x = r cos ⁡ θ e y = r sen ⁡ θ . Fazendo isso, teremos

r 1 2 = x 2 + y 2 = 1 ² + ( r 1 sen ⁡ θ ) ²

r 1 2 = 1 + r 1 2 sen ² ⁡ θ

r 1 ² ( 1 - sen ² ⁡ θ ) = 1

r 1 2 cos ² ⁡ θ = 1

r 1 cos ⁡ θ = 1

r 1 = 1 cos ⁡ θ

r 1 = sec ⁡ θ

Logo, os dois intervalos procurados são sec ⁡ θ ≤ r ≤ 2 e - π 3 ≤ θ ≤ π 3 . Usando a simetria da região R em relação ao eixo x, podemos integrar usando o intervalo 0 ≤ θ ≤ π 3 e depois multiplicar o valor da integral dupla por 2 . Boraaa calcular o valor desta área.

Passo 3

A = 2 ∫ 0 π 3 ∫ sec ⁡ θ 2 r   d r   d θ

= 2 ∫ 0 π 3 r 2 2 r = sec ⁡ θ 2 d θ

= ∫ 0 π 3 ( 4 - sec ² ⁡ θ )   d θ

= 4 θ θ = 0 π 3 - ∫ 0 π 3 sec ² ⁡ θ d θ

= 4 3 π - tg ⁡ θ θ = 0 π 3

= 4 3 π - 3

Resposta

A = 4 3 π - 3