Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 10.Problemas - Ex. 22

10.22. Calcule a reatância X tal que a impedância vista pela fonte seja real. Para este caso, calcule a corrente em regime permanente i(t) correspondente a I se w = 10 rad/s.

Passo 1

Fala pessoal, tudo bem com vocês?

Primeiramente vamos recordar aqui do circuito da nossa questão.

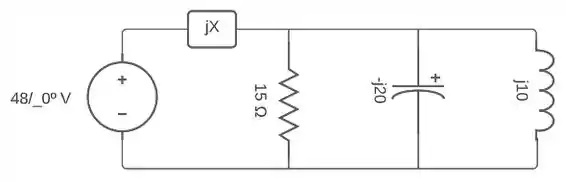
Vamos agora, calcular a resistência equivalente do circuito:

R e q → - 20 j 10 j 10 j - 2 0 j = 200 - 10 j = 20 j →

→ R e q = 20 j 1 5 20 j + 15 = 9,6 + 7,2 j

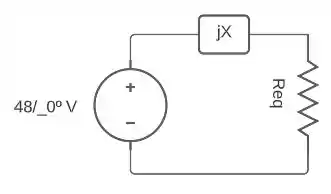
Sendo a parte imaginária = 0:

Z = j X + R e q → j X + 9,6 + 7,2 j = 9,6 →

→ X = - 7,2   Ω

Agora, é possível, calcular a corrente em regime permanente i ( t ) correspondente a I se w   =   10   r a d / s :

I = V Z = 48 ∠ 0 ° 9,6 = 5 ∠ 0 ° = 5 cos ⁡ ( 10 t ) A

Resposta

I = V Z = 48 ∠ 0 ° 9,6 = 5 ∠ 0 ° = 5 cos ⁡ ( 10 t ) A

Exercícios de Livros Relacionados

As expressões para a tensão e a corrente de regime permanente nos terminais do circuito da Figura P9.14 são vg = 300 cos (5.000pt + 78°) V, i g = 6 sen (5.000pt + 123°) A. a) Qual é a impedância vista
Uma tensão senoidal de 80 kHz tem ângulo de fase nulo e amplitude máxima de 25 mV. Quando essa tensão é aplicada aos terminais de um capacitor, a corrente resultante de regime permanente tem amplitude
a) Mostre que, a uma dada frequência v, os circuitos na Figura P9.18(a) e (b) terão a mesma impedância entre os terminais a,b se R 1 = ω 2 L 2 2 R 2 R 2 2 + ω 2 L 2 2 , L 1 = L 2 2 R 2 R 2 + ω 2 L 2 2
Calcule a função de rede Z(s) com uma entrada de soldagem através do resistor de 6 Ω da Figura 14.9 e use o resultado para encontrar as frequências naturais.