Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 10.Problemas - Ex. 24
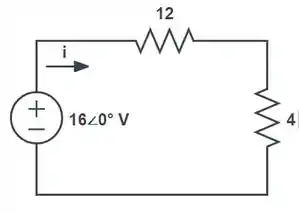
10.24. Calcule C tal que a impedância vista pela fonte seja real. Neste caso, calcule a potência absorvida pelo resistor de 12-Ω.
Passo 1
Vamos para um exercício, belezinha?
Primeiramente vamos recordar do circuito da nossa questão:
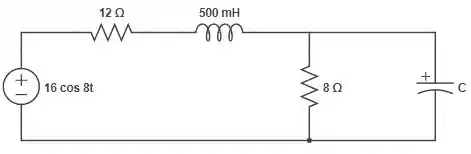
Vamos agora, calcular com o equivalente do circuito:
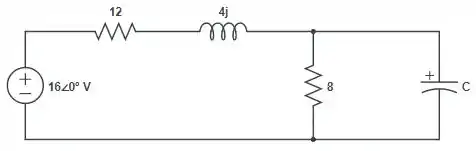
Sabendo que a impedância equivalente é:
E que a impedância vista pela fonte seja real, ou seja, a Parte imaginária de :
Sabe-se que:
Logo:
Da parte imaginária, temos que , é:
Passo 2
Agora, é possível, calcular a potência absorvida pelo resistor de :
Resposta
Exercícios de Livros Relacionados
Usando a figura 9.45 , elabore um problema para ajudar outros estudantes a entender melhor a admitância.
Para o circuito exibido na Figura 9.46 , determine Z e q e use esta para determinar a corrente I . Considere ω = 10r a d / s .
Usando a figura 9.43 , elabore um problema para ajudar outros estudantes a entenderem melhor a impedância.
No circuito da Figura 9.47 , determine i 0 quando: ω = 1r a d / s ; ω = 5r a d / s ; ω = 10r a d / s .
50- Determine v x no circuito da Figura 9.57 . Considere i s t = 5 cos 100 t + 40 ° A