10.40) Determine i(0) e v(0) no Prob. 10.39, tal que a componente natural desapareça e i seja simplesmente a componente forçada.
Passo 1
Bora para mais um exercício, galerinha???
Nosso circuito é mostrado abaixo:
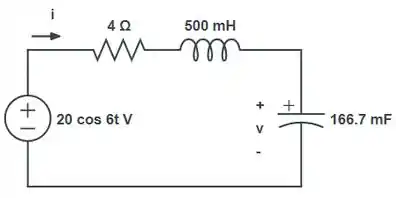
Podemos verificar que:
Fazendo LKT no circuito:
Substituindo por temos:
Passo 2
Agora, representando o circuito através de fasores:
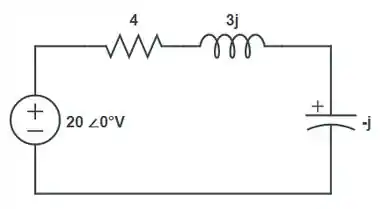
Sabendo que:
Sabendo que:
Logo, temos: