Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 12.Problemas - Ex. 6
12.6. Calcule a potência media absorvida pelo resistor de 6-Ω.
Passo 1
Eai, tudo joia? Vamos para mais uma questão!
Vejamos! A questão nos pede pra calcular a potência do seguinte circuito:
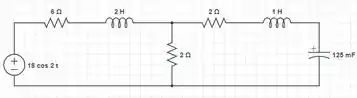
Equivalente a este circuito, podemos obter:
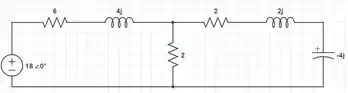
Sabendo que:
E que nossa resistência equivalente será:
Podemos encontrar a corrente do circuito, dada por:
A tensão no resistor de valor 6 Ω, é:
Logo, nossa Potência é calculada através da equação abaixo:
Agora, é só substituirmos os dados que já temos anteriormente:
Portanto, temos:
Resposta
Exercícios de Livros Relacionados
O valor de pico da tensão da fonte senoidal do circuito da Figura P10.48 é 180 V, e sua frequência é 5.000 rad/s. O resistor de carga pode variar de 0 a 4.000 V e o capacitor de carga pode variar de 0
a) Determine a relação de espiras N1/N2 do transformador ideal, no circuito da Figura P10.63, de modo que uma potência média máxima seja fornecida à carga de 400 V. b) Determine a potência média forne
A impedância ZL no circuito da Figura P10.54 é ajustada para máxima transferência de potência média a ZL. A impedância interna da fonte de tensão senoidal é 4 + j7 V. a) Qual é a máxima potência média
O resistor de 160 V no circuito da Figura P10.51 é substituído por uma impedância variável Zo. Admita que Zo seja ajustada para transferência de máxima potência média. a) Qual é a máxima potência médi
Determine a expressão de regime permanente para as correntes i g e i L no circuito da Figura P10.55, quando vg = 400 cos 400t V.Determine o coeficiente de acoplamento. c) Determine a energia armazenad