Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 18
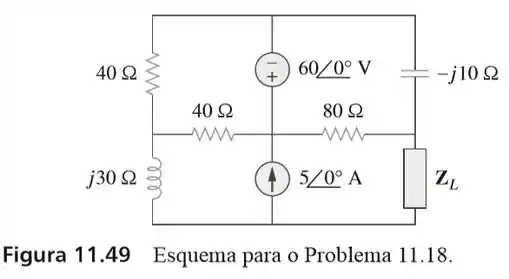
18. Determine o valor de no circuito da figura abaixo para a transferência de potência máxima.
Passo 1
Olha só! Para obter o valor de a fim de que ocorra a transferência de potência máxima, basta obter a impedância de , .
O conjugado da impedância de tem que ser igual a , para que essa condição seja satisfeita.
Por isso, vamos lá obter a impedância de . Vamos excluir a impedância , abrir o cicuito no ramo onde está circulando a fonte de corrente e substituir a fonte de tensão por um curto circuito.
Passo 2
De modo que o nosso circuito fica desse jeito aqui:
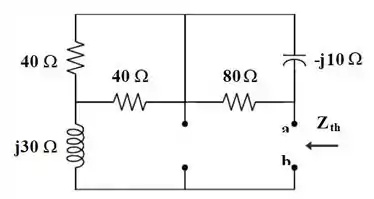
Por essa figura, fica fácil saber que a nossa impedância, , vai valer:
Consequentemente...
E voilà! Resposta encontrada!
Resposta
Exercícios de Livros Relacionados
O amp op no circuito da Figura P10.7 é ideal. Calcule a potência média fornecida ao resistor de 1 kV, quando v g=c o s1.000 tV .