Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 5.Problemas - Ex. 19
19- Determine no circuito da Figura .
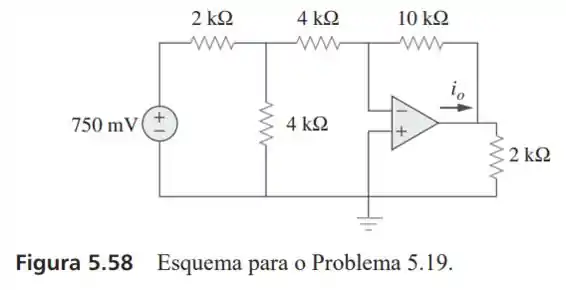
Passo 1
Pela tensão na porta não inversora ser zero temos que a tensão na porta inversora também será zero, e por conta de toda essa malha resistiva existir o que der para simplificar nós iremos simplificar. E a melhor maneira de simplificar esse circuito é primeiramente transformar a fonte de tensão e o resistor de em uma fonte de corrente de forma que agora teremos uma fonte de corrente de:
Nos deixando com o seguinte circuito.
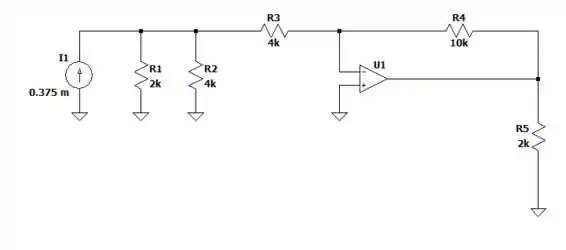
Dessa forma os resistores de e de estão em paralelo. Fazendo a resistência equivalente desses dois resistores nós teremos:
Deixando nosso circuito da seguinte forma:
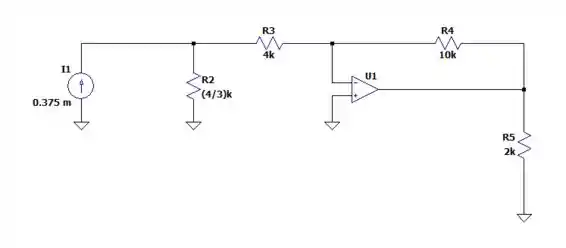
Já que a resistência equivalente ocupa os mesmos pontos dos dois resistores que a formam.
Voltando agora para a fonte de tensão nós teremos:
O que nos dá um circuito igual a:
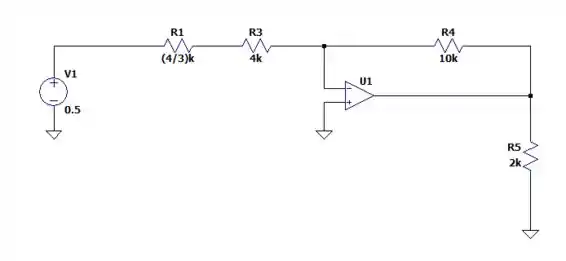
Passo 2
Agora vamos ver qual a tensão na saída do amplificador operacional e as correntes que passam pelas resistências.
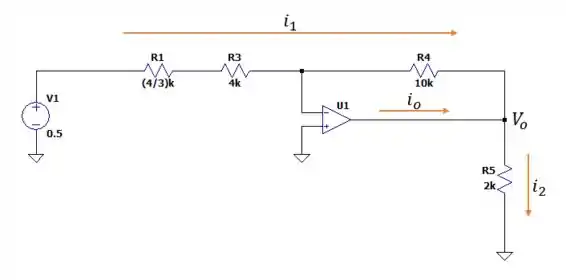
Esse tipo de amaplificador é tal que temos a seguinte relação:
Ou seja:
Passo 3
E pela análise de correntes conseguimos ver que:
Onde as correntes são encontradas por:
E:
Logo: