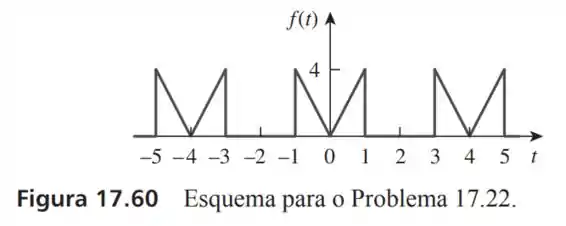
22- Calcule os coeficientes de Fourier para a função da Figura .
Passo 1
O período da onda do meio começa em e termina em , logo o período dessa onda é de:
O que nos dá um de:
E as equações dentro desse período são:
Passo 2
Dessa forma o coeficiente será:
Note que podemos dizer que:
Passo 3
Agora para :
Fazendo a integração por partes:
Passo 4
Agora :
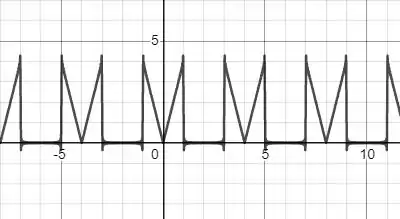
Pela reta ser decrescente no lado negativo e crescente no lado positivo do eixo horizontal nós conseguimos ver que a função é par, portanto não há . Matematicamente isso pode não ser verificado, mas acredite quando colocamos e os parâmetros que encontramos nós encontramos o seguinte gráfico para pontos. Então a teoria se faz correta.