Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 15.Problemas - Ex. 26
Altere em escala a impedância e a frequência no circuito do Prob. e para obter um filtro passa-faixa com freqüência central , com índice de mérito usando um capacitor de (Sugestāo: Veja o Prob. 15.9.)
Passo 1
E ai pessoal tudo bem? O enunciado pede que a gente determine alterar em escala a impedância e a frequência no circuito do Prob. e
Começamos esboçando o circuito 😊
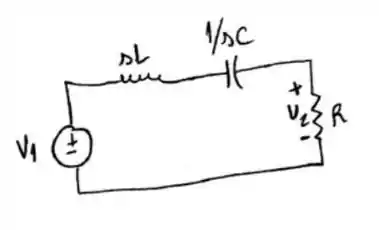
Agora temos que relacionar as tensões V1 e V2
Passo 2
Alterando a escala
Resposta
R =
Exercícios de Livros Relacionados
Troque a função de excitaçảo real I m c o s ω t no Ex. 10.2 . 2 pela funçáo de excitaçăo complexa I m e jwl . Calcule a resposta complexa resultante v 1 e mostre que a resposta real é v = R e v 1
(a) Das equações no domínio do tempo, calcule a resposta forçada v se v g = 10 e β tV .
Determinar se v 1 está adiantada ou atrasada em relaçáo a v 2 e de quanto.(a) v 1 = 3 c o s 4 t - 30 ∘ , v 2 = 5 s e n 4 t ,
Converta as seguintes funçōes para funçōes coseno com amplitudes positivas:(a) 6 s e n 2 t + 15 ∘ , (b) - 2 c o s 4 t + 10 ∘ , (c) 8 c o s 5 t - 15 s e n 5 t .
Calcule i 4 , usando somente as propriedades das senóides se ( b ) i 1 = 5 c o s 3 t + 30 ∘ A , i 2 = 5 s e n 3 tA , e i 3 = 5 c o s 3 t + 150 ∘ A