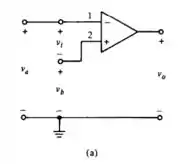
Um amp. op. nõo-ideal mostrado em (a) pode ser representado pelo modelo de (b), onde A é um ganho muito elevado, da ordem de 10^5 . Para amp. op de alta qualidade, o ganho deve ser muito maior, da ordem de 10^8 ou superior. (Um modelo mais sofisticado tem um resistor entre os terminais 1 e 2 em (b), de modo que as correntes de entrada não sejam exatamente zero. Esta resistência deve ser de valor muito elevado - (10^5 a 10^15), que será representada como um circuito aberto.) Finalmente, como V1 = V0/A e A é extremamente elevado, V1 tende a zero. No caso ideal (A ) V1 = 0, como bem sabemos. (a) Mostre que, para um amplificador não-ideal, o seguidor de tensão da Figura 3.13 tem a saída: v2 = Av1/(1+A) e então para o caso ideal, V2 = VI (b) Calcule V2 para casos em que A = 10^5, 100 e 1.

Então bora láa!!

Vamos para a letra a)

Um caso especial é o caso em que (curto-circuito) e (circuito aberto), mostrado na Figura 3.13. Este circuito tem , ou e é denominado de seguidor de tensão, isto é, segue . Ele também é chamado um amplificador "buffer", pois pode ser usado para isolar um circuito de outro. (A tensão nos dois pares de terminais é a mesma, mas não há circulação de corrente de um par para outra.)

Sendo assim

Para o caso ideal, como e

Portanto

Agora vamos para o último passo!!

Na letra b)

Considerando a fórmula encontrada em a)

Para

Para

Para

Pronto!!