Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 9.9 - Ex. 1

Assuma que R = 6   Ω , L = 1   H , v g = 0 , v 0 = 8   V e i 0 = 4   A na fig 9.10. Calcule i para t > 0 , se C é

a) 1 5 F

b) 1 34 F

c) 1 9 F

Passo 1

Oioiiii gentee

Se liga, temos esse circuitinho aqui:

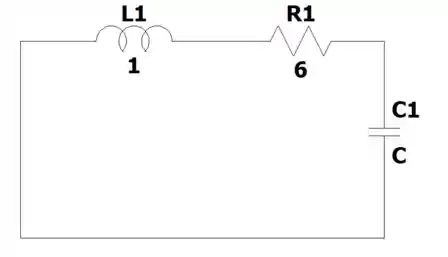
Onde v 0 = 8   V e i 0 = 4   A

Aí nesse exercício, vamos variando os valores de C para calcularmos a expressão da corrente que passa pelo circuito para t > 0 , fechou?

Mas antes de tudo, vamos calcular o valor de 4 L R 2 , pois é o valor ♥ com quem vamos comparar C para saber sobre o amortecimento do circuito:

♥ = 4 L R 2

♥ = 4 × 1 36 ≅ 0,1

Além disso, a equação genérica para encontrar a corrente t > 0   em um circuito RLC em série, fazendo a LKT no circuito, vai ser

L d i d t + R i + 1 C ∫ 0 t i   d t + v ( 0 ) = v g

Com equação característica:

L s 2 + R s + 1 C = 0

Agora sim, vamos lááá

Passo 2

a) Para C = 1 5 F , nossa equação fica assim

1 d i d t + 6 i + 5 ∫ 0 t i   d t + 8 = 0

Dessa forma, a equação característica fica assim:

s 2 + 6 s + 5 = 0

Vamos encontrar as raízes dessa equação que são as frequências fundamentais do circuito:

∆ = 6 2 - 4.1 . 5 = 16

s 1 = - 6 + 4 2 = - 1

s 2 = - 6 - 4 2 = - 5

Logo, nossas raízes são s 1,2 = - 1   e - 5

Passo 3

Agora chegou o grande momento de compararmos o valor de C com o valor de ♥ que calculamos lá no passo 1

Temos que

C = 1 5 = 0,2

Enquanto ♥ = 0,1

Dessa forma, temos que C > ♥ , e portanto, o circuito é superamortecido

Isso indica que a sua resposta será dada assim olha:

i t = A 1 . e s 1 t + A 2 . e s 2 t

Passo 4

Substituindo os valores de s 1 e s 2 na resposta do circuito, temos

i t = A 1 . e - t + A 2 . e - 5 t

Boaaa, agora é só encontrar os valores de A 1 e de A 2 :D

Primeiramente, sabemos que i 0 = 4 , ou seja:

i 0 = A 1 . e 0 + A 2 . e 0 = 4

A 1 + A 2 = 4

Além disso, d i d t ( 0 ) = v ( 0 + ) :

d i d t 0 = - A 1 . e 0 - 5 A 2 . e 0 = 8

- A 1 - 5 A 2 = 8

Passo 5

Juntando as duas equações que encontramos no passo 4, montamos o sistema

A 1 + A 2 = 4 - A 1 - 5 A 2 = 8

Somando as duas equações, temos

- 4 A 2 = 12

A 2 = - 3

Substituindo na primeira:

A 1 - 3 = 4

A 1 = 7

Portanto, a corrente i vai ser

i t = 7 . e - t - 3 . e - 5 t

Passo 6

b) Para C = 1 34 F , nossa equação fica assim

1 d i d t + 6 i + 34 ∫ 0 t i   d t + 8 = 0

Dessa forma, a equação característica fica assim:

s 2 + 6 s + 34 = 0

Vamos encontrar as raízes dessa equação que são as frequências fundamentais do circuito:

∆ = 6 2 - 4.1 . 34 = - 100

s 1 = - 6 + 10 j 2 = - 3 + 5 j

s 2 = - 6 - 10 j 2 = - 3 - 5 j

Logo, nossas raízes são s 1,2 = - 3 ± 5 j

Passo 7

Agora chegou o grande momento de compararmos o valor de C com o valor de ♥ que calculamos lá no passo 1

Temos que

C = 1 34 = 0,02

Enquanto ♥ = 0,1

Dessa forma, temos que C < ♥ , e portanto, o circuito é subamortecido

Nesse caso, a frequência de ressonância é

ω 0 = 1 L C = 1 1 × 1 34 = 5,83

O coeficiente de amortecimento será

α = R 2 L = 6 2 = 3

E a frequência amortecida será

ω d = ω 0 2 - α 2 = 5,83 2 - 3 ² = 5

E dessa forma, a resposta do circuito é

i t = e - α t A 1 . cos ⁡ ω d t + A 2 . s e n ω d t

Passo 8

Substituindo os valores na resposta do circuito, temos

i t = e - 3 t A 1 . cos ⁡ 5 t + A 2 . s e n 5 t

(repara que o valor no expoente do Euler é a parte real das raízes, e o valor no seno e cosseno é a parte imaginária)

Boaaa, agora é só encontrar os valores de A 1 e de A 2 :D

Primeiramente, sabemos que i 0 = 4 , ou seja:

i 0 = e - 3 × 0 A 1 . cos ⁡ 0 + A 2 . s e n 0 = 4

A 1 = 4

Além disso, d i d t ( 0 ) = v ( 0 + ) :

d i d t 0 = - 3 . e - 3 × 0 . A 1 . cos ⁡ 0 + A 2 . s e n 0 + e - 3 × 0 - 5 A 1 . sen ⁡ 0 + 5 A 2 . c o s 0 = 8

- 3 A 1 + 5 A 2 = 8

Substituindo o valor de A 1 = 4 , temos

- 12 + 5 A 2 = 8

5 A 2 = 20

A 2 = 4

Passo 9

Agora que encontramos os valores de A 1 e A 2 , é só substituir:

i t = e - 3 t A 1 . cos ⁡ 5 t + A 2 . s e n 5 t

i t = e - 3 t 4 . cos ⁡ 5 t + 4 . s e n 5 t

Fechou?? 😊

Passo 10

c) Para C = 1 9 F , nossa equação fica assim

1 d i d t + 6 i + 9 ∫ 0 t i   d t + 8 = 0

Dessa forma, a equação característica fica assim:

s 2 + 6 s + 9 = 0

Vamos encontrar as raízes dessa equação que são as frequências fundamentais do circuito:

∆ = 6 2 - 4.1 . 9 = 0

s = - 6 2 = - 3

Logo, só temos uma raíz, e ela vale - 3

Passo 11

Agora chegou o grande momento de compararmos o valor de C com o valor de ♥ que calculamos lá no passo 1

Temos que

C = 1 9 = 0,1

Enquanto ♥ = 0,1

Dessa forma, temos que C = ♥ , e portanto, o circuito é criticamente amortecido

Isso indica que a sua resposta será dada assim olha:

i t = A 1 + A 2 t . e s t

Passo 12

Substituindo o valor de s na resposta do circuito, temos

i t = A 1 + A 2 t . e - 3 t

Boaaa, agora é só encontrar os valores de A 1 e de A 2 :D

Primeiramente, sabemos que i 0 = 4 , ou seja:

i 0 = A 1 + A 2 × 0 . e - 3 × 0 = 4

A 1 = 4

Além disso, d i d t ( 0 ) = v ( 0 + ) :

d i d t 0 = A 2 . e - 3 × 0 + A 1 + A 2 × 0 × - 3 e - 3 × 0 = 8

A 2 - 3 A 1 = 8

Substituindo A 1 = 4 :

A 2 - 12 = 8

A 2 = 20

Passo 13

Substituindo os valores de A 1 e A 2 na resposta do circuito, encontramos:

i t = 4 + 20 t . e - 3 t

E acabaaaamoss

Resposta

a) i t = 7 . e - t - 3 . e - 5 t

b) i t = e - 3 t 4 . cos ⁡ 5 t + 4 . s e n 5 t

c) i t = 4 + 20 t . e - 3 t