Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 2.2 - Ex. 1
CaIcule e .
Passo 1
Falaaaa, galeraaaa!
Na imagem abaixo temos o circuito em questão e os pontos , , e .
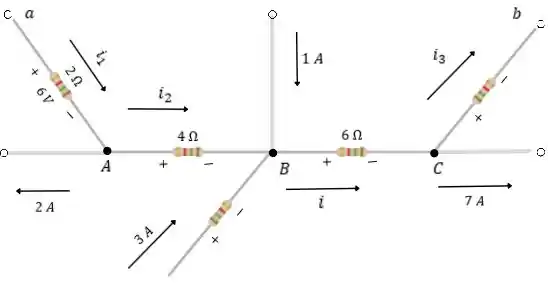
Para resolver essa questão devemos aplicar as Leis de Kirchhoff. Temos:
- Lei de Kirchhoff das tensões(LKT): “A soma das tensões em torno de uma malha fechada é zero”.
- Lei de Kirchhoff das correntes(LKC): “A soma de todas as correntes que chegam a um nó do circuito deve ser igual à soma de todas as correntes que deixam esse mesmo nó.”
Passo 2
Primeiramente, vamos aplicar a LKC no ponto :
Aplicando a LKC em , obtemos:
Por fim, aplicando LKC em , obtemos:
Passo 3
De posse das equações (I), (II) e (III), podemos encontrar as correntes que passam pelo circuito.
Calculando , temos:
Então,
Da expressão , temos:
Da expressão , temos:
Da expressão (III), temos:
Passo 4
Aplicando a LKT em (sentido horário):
Agora podemos isolar , obtendo:
Substituindo os valores de corrente encontrados no passo 3, temos:
Prontinho!
Resposta
Exercícios de Livros Relacionados
Para a rede da figura 2.89 , determine a corrente, a tensão e a potência associadas ao resistor de 20k Ω .
A partir do circuito da figura 2.83 , determine I , a potência dissipada pelo resistor e a potência fornecida por cada fonte.
No circuito mostrado na figura 2.87 , determine v x e a potência absorvida pelo resistor de 12 Ω .
Determine V_0 no circuito da figura 2.80 .
No circuito da figura 2.75 , calcule v_1 , v_2 e v_3 .