Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.Problemas - Ex. 27
Se , calcule e
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
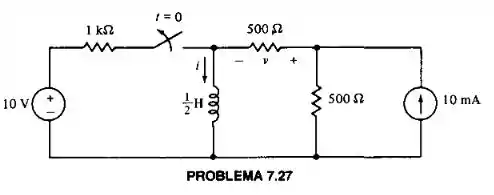
Vamos lá, vamos analisar para , que é o tempo antes da chave abrir, como está em regime permanente, o indutor se comporta como um curto circuito, logo, no segmento em que o indutor está teria apenas o fio. O problema quer descobrir , e a corrente no indutor não varia de maneira brusca, logo
Logo, para o intervalo de , nós temos a seguinte configuração de circuito:
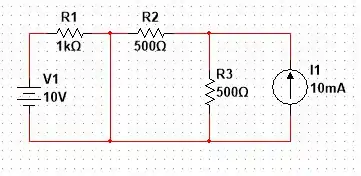
Agora, nós queremos saber das correntes que passam pelos resistores e , vamos chamar por e respectivamente. No nó do indutor, as correntes e estão entrando no nó e a corrente do indutor está saindo do nó, logo:
Ok, agora vamos descobrir as duas correntes, para temos uma fonte de tensão e um resistor, como são elementos lineares, podemos usar a Lei de Ohm para fazer os cálculos, com isso, nós obtemos o seguinte resultado
Substituindo os valores, nós temos que
Vamos analisar a corrente , a fonte de corrente passa pelo nó do resistor , com isso, temos que pegar o paralelo com o resistor de , com isso, nós temos que
Logo, será igual a
Passo 2
Para o caso de , nós temos a seguinte configuração de circuito
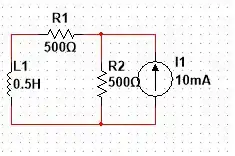
Usando a LKC no nó, temos que
Sendo que a corrente no indutor não muda, logo
Com isso, podemos descobrir a tensão no resistor , com isso
E no caso de ...
Passo 3
Para encontrar a tensão no indutor, vamos fazer a LKT na malha, com isso, nós temos que
Logo
Substituindo os valores, nós temos que
Revisitando a fórmula para o indutor, nós temos que
Então
Fazendo a substituição de valores, percebemos que