Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.Problemas - Ex. 24
Se v(0-) = 12 V, calcule wL (0+) e di(0+)/dt
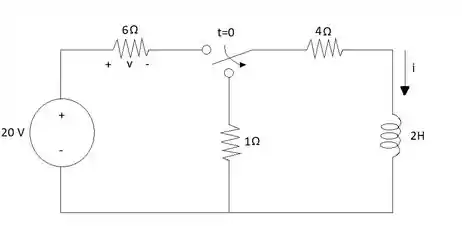
Passo 1
E aí galera, tudo bem? Vamos resolver mais uma questão aqui com vocês.
Antes de tudo devemos prestar atenção ao que está sendo especificado no enunciado da questão e ter cuidado caso exista alguma pegadinha. Visto que no momento inicial o enunciado não fala que o circuito estava em regime permanente, não se deve substituir o indutor por um curto-circuito.
Para poder encontrar os valores no instante é necessária ter conhecimentos dos valores no instante .
Considerando-se ainda que no instante é que ocorre a troca de posição da chave, se diz que no instante o circuito se encontra da seguinte forma:
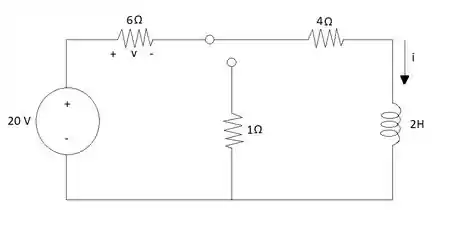
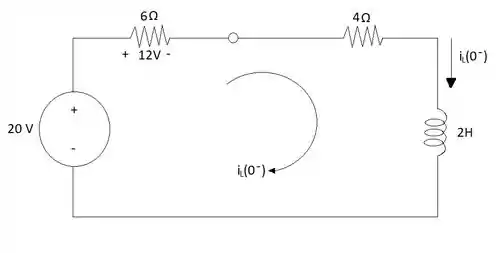
Como uma parte do circuito não é fechada então ele é desconsiderado dos cálculos.
Dessa forma podemos encontrar o valor da corrente usando o dado do enunciado que diz que :
Por causa dos princípios físicos com os quais os é feito um indutor se sabe que após ele ter sido carregado energeticamente ele não permite mudanças significativas nessa energia que é armazenada na forma de corrente. Dito isso pode-se afirmar o seguinte:
Passo 2
Com o valor de que foi encontrado anteriormente é possível realizar o cálculo de da seguinte forma:
Passo 3
Para encontrar o valor de precisamos ver como é que o circuito se encontra no instante
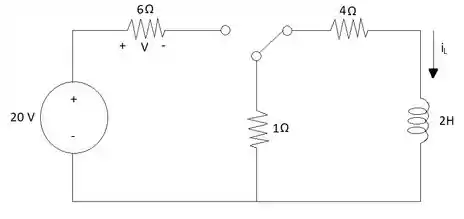
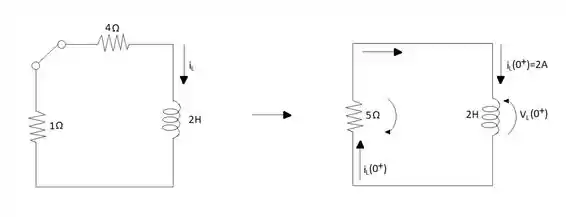
Visto que o circuito final é aquele apresentado na figura, precisamos levar em consideração que a equação para o nosso caso pode ser escrito como . Dessa forma vemos que é necessário encontrar o valor de para poder resolver a equação.
Para encontrar no circuito é necessário encontrar a tensão no resistor e depois aplicar LKT. Por cálculos básicos de eletricidade sabemos que a tensão do resistor é de 10 V e usando LKT no circuito temos o seguinte para :
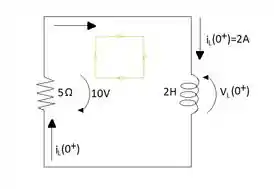
Com esse dado podemos encontrar o segundo item da questão: