Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.Problemas - Ex. 36
8.36) Calcule v para t > 0, se vg = 2e-3t V e vC(0) = 0.
Passo 1
E aí galerinhaaa!! Vamos resolver essa questão juntinhos, beleza??
Nosso circuito é mostrado abaixo:
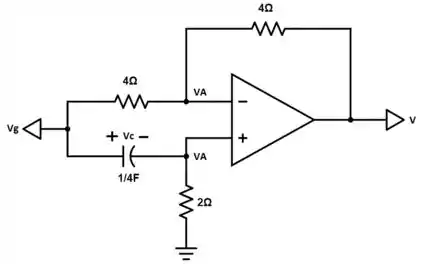
Primeiro, levando em consideração que o amplificador é ideal, temos que as tensões nas entradas inversora e não-inversora devem ser iguais.
Começando a analisar o circuito pelo terminal positivo do Amp. Op. verificamos:
Porém,
Substituindo (2) e (3) em (1) temos:
Substituindo por em (4):
Logo, a equação que representa é:
Precisamos achar agora o coeficiente A, mas como?? Sem estresse! Basta utilizar a condição inicial dada ():
Chegamos que:
Passo 2
Agora, vamos analisar o circuito do terminal inversor do Amp. Op. Fazendo LKC temos:
Utilizando (1) e (3) em (6) obtemos:
Encontrando através de (5):
Substituindo (5) e (8) em (7), chegamos por fim, na equação de v(t):
Prontinhooo, essa teve muito cálculo, mas deu pra pegar a ideia, né? Bora pra mais uma??