Calcule o equivalente de Thevenin de tudo, exceto o resistor de no Prob. 5.16, e use o resultado para encontrar a potência entregue ao resistor de .
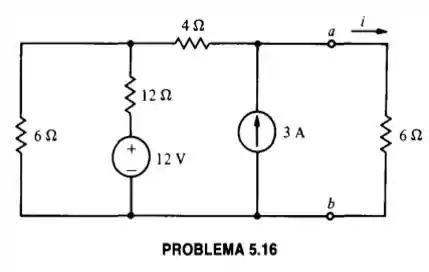
Passo 1
E aewww pessoal, tudo bem?
Seguinte, nessa questão de novo vamos ter que apelar pro Teorema de Thevenin e em seguida, achar a corrente circulando no resistor de pra encontrar a potência...
Pois muito bem! Como sabemos, nesse circuito temos duas fontes de tensão independentes...
Vamos então, excluir elas... A fonte de tensão de vira um curto circuito e a fonte de corrente de vira um circuito aberto...
Com isso, a resistência equivalente vai ser dada por...
Lembrando que dessa vez, estamos trabalhando com o resistor de , não o de
Passo 2
Agora, pra achar , vamos apelar pro teorema da transformação de fontes...
Como já falamos, temos duas fontes independentes... Temos que trabalhar com elas
Vamos então, usar o método de transformação de fontes...
Por esse método, aquela fonte de tensão de em série com o resistor de , acaba dando origem a uma fonte de corrente de...
Que acaba ficando em paralelo com o resistor de ...
E tem também aquela fonte de corrente de que está em paralelo com o resistor de ... Isso acaba virando uma fonte de tensão de em série com esse mesmo resistor de
Do seguinte jeitinho abaixo
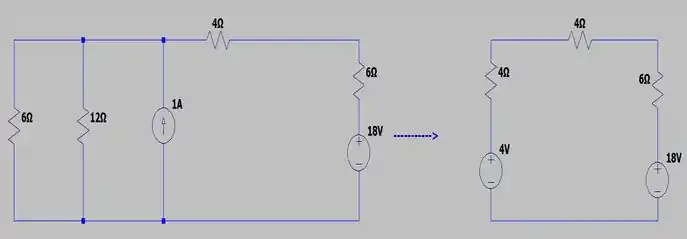
Passo 3
Aí, pra achar a corrente circulando no resistor de , vamos aplicar a análise de tensões em uma malha...
A potência dissipada nesse resistor vai valer então,
Pronto, guys! Missão cumprida!