Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 11.3 - Ex. 3
Calcule , e na Fig. 11.15.
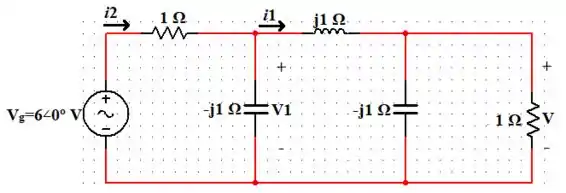
Passo 1
Falaeee! Seguinte, vamos reduzir o circuito dado da seguinte forma:
Primeiro vamos fazer o paralelo da resistência ali da direita com a reatância do capacitor:
Assim, o circuito fica:
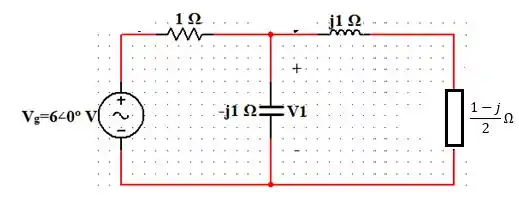
Somando a impedância descoberta anteriormente com o a reatância indutiva, temos:
Assim, o circuito fica:
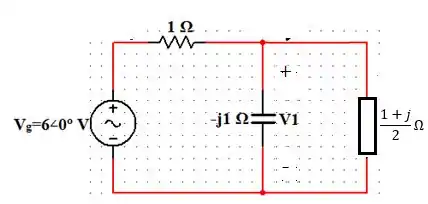
Percebemos que a impedância e a reatância capacitiva estão em paralelo, ou seja, possuem a mesma tensão em seus terminais.
Assim, fazendo o paralelo entre eles, temos:
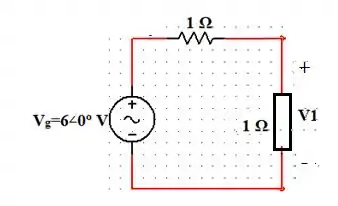Ou seja:
Assim, podemos ver que a queda de tensão será igual no resistor e na impedância, o que podemos confirmar que !!!!
Obs: a impedância equivalente é igual a soma da resistência com a impedância que encontramos anteriormente, ou seja, . ;)
Passo 2
Com isso, basta usar a Lei de Ohm para descobrirmos o valor de (vale lembrar que a impedância equivalente é de 2). Assim temos:
Passo 3
Pela Lei dos Nós, podemos determinar . Vamos pegar apenas o trecho do circuito que queremos para ficar mais fácil nossa análise rsrsrs:
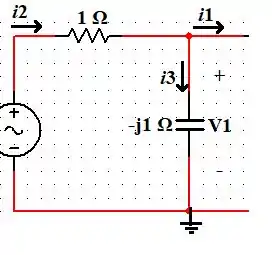
Percebemos que:
Muito simples nee?? Valeeeu!!